三平方の定理は、直角三角形における基本的な幾何学的関係を示す公式です。
「ピタゴラスの定理」とも呼ばれ、設計の寸法計算や機械要素の位置決め、力学解析など、幅広い場面で活用されます。
この記事では、三平方の定理の基礎から具体的な応用例まで解説します。
三平方の定理の基礎知識
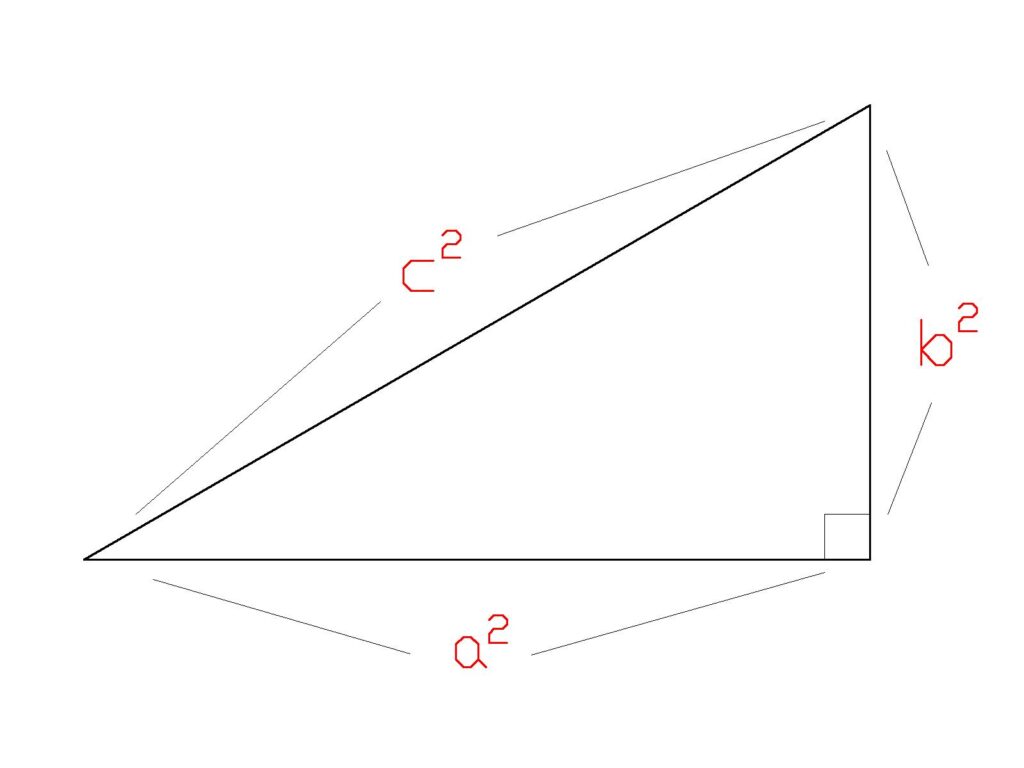
三平方の定理は次のように定義されます。
直角三角形において、斜辺の長さの2乗は、他の2辺の長さの2乗の和に等しい。
公式としては以下の通りです。
\( \displaystyle c^2=\frac{a^2} {b^2}\)
ここで、
- c: 斜辺（直角を挟む最も長い辺）
- a, b: 直角を挟む他の2辺
機械設計における三平方の定理の必要性
寸法設計や部品配置に活用
斜め寸法の計算
直交する部品の間に斜めの部材を配置する際、三平方の定理を使うことで正確な長さを計算可能。
ダクトや配管の長さ
配管の直角コーナー部や機械フレームの対角線長を求める際に利用。
力の分解と合成
- 斜めに作用する力の分解
- 斜め方向の力を水平成分と垂直成分に分解する際、三平方の定理を利用して力の大きさを計算。
- 結果力の合成
- 複数の力が異なる方向に作用している場合、合成力の大きさや方向を求める際に活用。
三平方の定理の応用例
例1: 直交するフレームの対角線長さ
問題設定
幅200mm、高さ300mmの直交するフレームがあります。このフレームの対角線の長さを計算します。
解法
三平方の定理を適用
\( \displaystyle c^2=a^2+b^2\)
\( \displaystyle c^2=200^2+300^2\)
\( \displaystyle c^2=40000+90000=130000\)
\( \displaystyle c= \sqrt {130000}≈360.55mm\)
結果
対角線の長さは 約360.55mm です。
例2: スロープの斜辺の計算
問題設定
高さ2mの荷物を運ぶため、水平距離5mのスロープを設置します。スロープの長さを求めます。
解法
三平方の定理を適用
\( \displaystyle c^2=a^2+b^2\)
\( \displaystyle c^2=2^2+5^2\)
\( \displaystyle c^2=4+25=29\)
\( \displaystyle c= \sqrt {29}≈5.39m\)
結果
スロープの長さは 約5.39m です。
例3: 力の合成
問題設定
ある部品に水平方向へ100N、垂直方向へ50Nの力が同時に作用しています。この2つの力を合成した合力の大きさを計算します。
解法
合力 F の大きさは次式で計算
\( \displaystyle F^2=Fx^2+Fy^2\)
\( \displaystyle F^2=100^2+50^2=10000+2500=12500\)
\( \displaystyle F= \sqrt {12500}≈111.8N\)
結果
合成力の大きさは 約111.8N です。
三平方の定理を使う際の注意点
- 単位を統一する
- 計算する際、各辺の長さや力の単位を統一しておく必要があります。
- 例えば、mmとmを混在させると計算ミスにつながります。
- 直角三角形であることを確認
- 三平方の定理は直角三角形にのみ適用できます。
- 問題に与えられた角度や条件を確認しましょう。
- 平方根の近似値
- 計算で平方根を含む場合、必要に応じて適切な桁数で近似値を取ります。
- 過剰な桁数の計算は工数が増える原因となります。
平方根（√）について
平方根 （√） は、機械設計において幾何学計算や力学解析の際に頻繁に登場する基本的な数学概念です。斜辺や対角線の長さを求める場面や、断面係数の計算など、設計のあらゆる場面で活用されます。
平方根の計算を効率化するためのポイント
基本的な値を覚える
設計現場では即座に平方根を計算できることが求められる場合があります。以下のような基本的な平方根は暗記しておくと便利です。
以下は平方根（√）の1～10までの値を小数第3位までで表にまとめたものです。
| 数値 (n) | 平方根 (√n) |
|---|---|
| 1 | 1.000 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3.000 |
| 10 | 3.162 |
- 平方根 （√） は、数値 n を自乗して元の数になる数を表します。
- この表は、手計算や設計時の概算に役立てることができます。
必要に応じて、この値を覚えておくと計算効率が向上します。さらに大きな数の平方根が必要であれば、計算機を利用するか、近似値を利用する方法があります。
概算技術を身につける
正確な平方根が不要な場合、近似計算を使って素早く見積もるスキルを身につけましょう。
計算ツールを補助的に使う
手計算が難しい場合は、CADや計算ツールを活用することで正確な値を得られます。ただし、手計算の基礎知識を持っていることで結果の妥当性を確認できます。
まとめ
三平方の定理は、機械設計において寸法設計や力学解析を行う際に不可欠な知識です。複雑な幾何学的形状や力の分解を計算する際、設計の精度を確保するために役立ちます。
- 具体例の活用
- 実際の設計業務でよくある問題を考慮し、三平方の定理を積極的に使いましょう。
- 手計算の練習
- CADや計算ツールを使う場合でも、まずは手計算で概算を出します。
- その結果の妥当性を確認する習慣をつけることが大切です。
三平方の定理をしっかりと理解し、実務で応用できるようになることで、設計の効率化と精度向上を実現しましょう！
コメント