機械設計において、構造物のたわみは安全性や機能に大きく影響を与えるため、設計時にしっかりと計算し確認する必要があります。特に梁は、機械や構造物の中で荷重を支える重要な要素です。梁のたわみ計算を適切に行うことで、材料の使用量を最適化し、無駄なコストを抑えながら強度と耐久性を確保することが可能です。
本記事では、梁のたわみ計算における基本的な理論や計算式について解説します。
梁のたわみとは？
たわみとは、梁に荷重がかかることで発生する曲げ変形のことを指します。たわみが過度に大きくなると、機械や構造物の性能が低下し、最悪の場合は破損や事故の原因となることがあります。設計段階でたわみを適切に計算することにより、設計の安全性と効率性を確保することができます。
たわみの基本原理
たわみの計算は、梁の支持条件や荷重条件によって異なりますが、基本的な理論として、梁の曲げ応力や曲げモーメント、ヤング率、断面二次モーメントが関係します。梁にかかる荷重とその結果として生じるたわみは、以下のように計算されます。
たわみの計算式
たわみ計算に使われる基本的な式は、ベルヌーイ・オイラーの梁理論に基づいており、次の式が使用されます。
\( \displaystyle δ=\frac{FL^3} {3EI}\)
δ：たわみ量（mm）
F：荷重（N）
L：梁の長さ（mm）
E：ヤング率（N/mm²）
I: 断面二次モーメント（mm⁴）
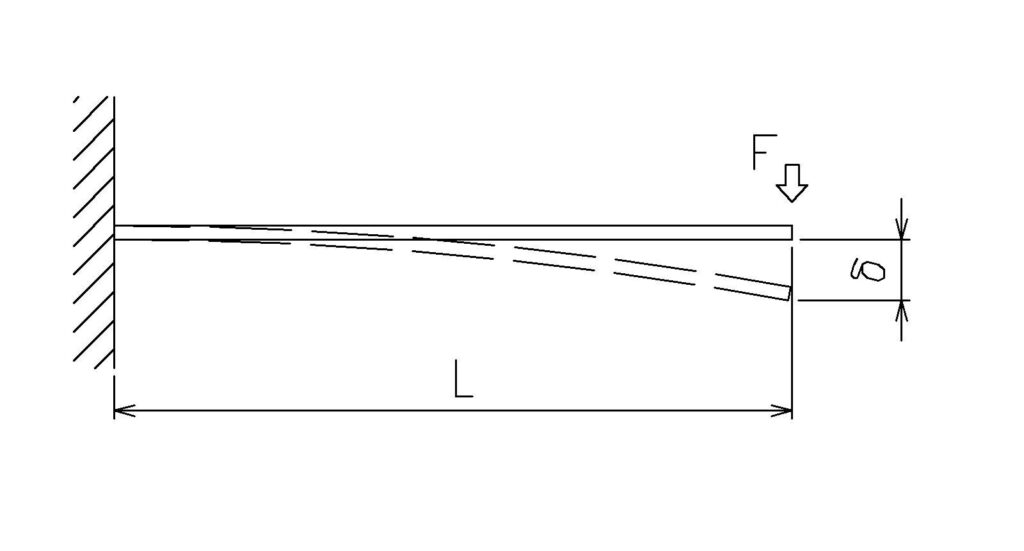
上記の式は、片持ち梁に集中荷重がかかる場合のたわみを計算するための基本的なものです。支持条件や荷重条件が変わると、たわみの計算式も変わります。
支持条件と荷重条件によるたわみ計算
梁のたわみは、支持方法と荷重の種類によって異なります。以下に、代表的な支持条件と荷重条件におけるたわみ計算式を紹介します。
片持ち梁に集中荷重がかかる場合
片持ち梁（片方が固定され、他方が自由な状態）に荷重がかかる場合、最大たわみは梁の自由端で生じます。
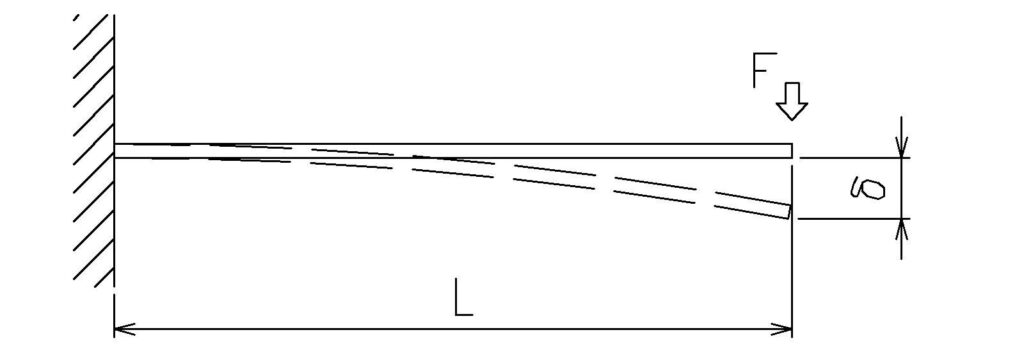
\( \displaystyle δ=\frac{FL^3} {3EI}\)
両端支持梁に集中荷重がかかる場合
両端が固定されている梁に中央に集中荷重がかかる場合の最大たわみは次の式で表されます。
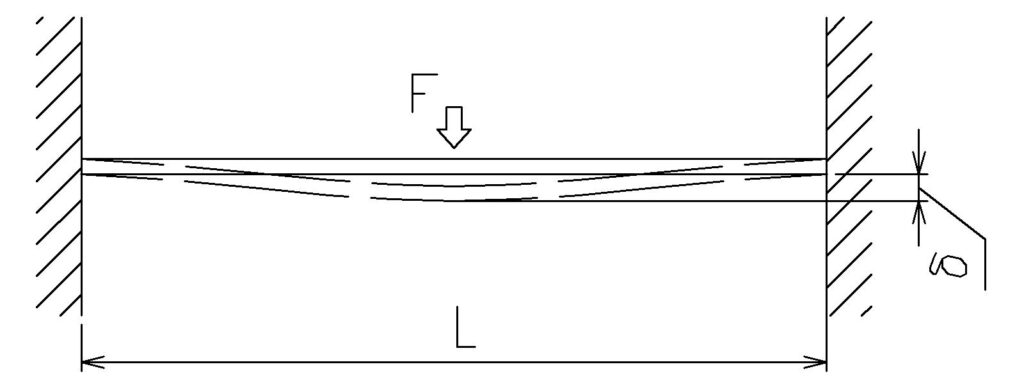
\( \displaystyle δ=\frac{FL^3} {48EI}\)
この場合、たわみは中央で最大となります。
片持ち梁に均等分布荷重がかかる場合
片持ち梁（片側が固定されている梁）において、荷重が梁全体に均等に分布している場合、たわみの計算は以下の式で求められます。この場合、たわみは梁の自由端で最大となります。
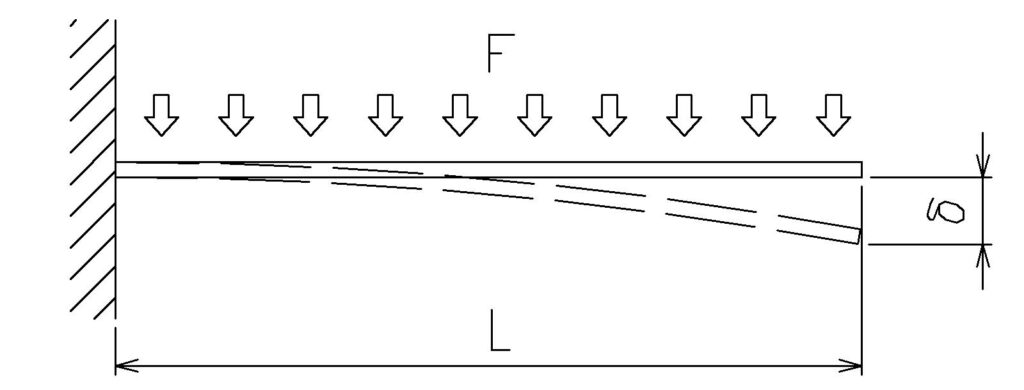
\( \displaystyle δ=\frac{wL^4} {8EI}\)
w: 単位長さあたりの荷重（N/mm）
均等分布荷重の計算は材料自身の自重によるたわみにも使用されます。
集中荷重がかかる場合は荷重によるたわみと自重によるたわみを考慮しよう！
両端支持梁に均等分布荷重がかかる場合
両端支持梁において、荷重が均等に分布している場合（全体にかかる荷重が均等な場合）、たわみの式は次のようになります。
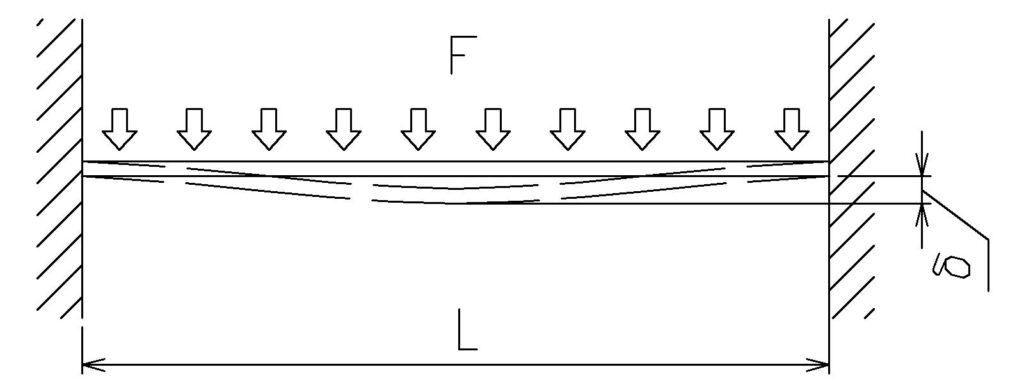
\( \displaystyle δ=\frac{5wL^4} {384EI}\)
w: 単位長さあたりの荷重（N/mm）
片持ち梁と両端支持梁の比較と使い分け
梁の設計において、たわみの計算は安全性や性能を確保するために重要なステップです。特に片持ち梁と両端支持梁は設計においてよく用いられる形式であり、それぞれに特性や使用場面があります。本項では、片持ち梁と両端支持梁の違い、特性、そして使い分けについて解説します。
片持ち梁と両端支持梁の基本構造
片持ち梁
片端が固定され、もう一方が自由端となる梁。
特徴
- 自由端に荷重を受ける場合、大きなたわみと応力が発生しやすい。
- 設計がシンプルで、片側からのアクセスが容易。
使用例: クレーンのアーム、壁から突き出した看板、キャントレバー型の棚。
両端支持梁
両端が支持されており、荷重が中間または特定の位置にかかる梁。
特徴
- 荷重が両端に分散されるため、たわみと応力が片持ち梁に比べて小さい。
- 荷重が均等に分布する場合に最適。
使用例: 橋梁、建物の床板、機械フレームの支持部。
特性の比較表
| 特性 | 片持ち梁 | 両端支持梁 |
|---|---|---|
| 構造 | 片端固定、もう片方は自由 | 両端支持 |
| たわみの傾向 | 梁の長さ L3に比例 | 梁の長さ L3に比例（片持ち梁より小さい） |
| 荷重の分散 | 荷重が固定端に集中 | 荷重が両端に分散 |
| 応力 | 応力が固定端に集中 | 応力が梁全体に分散 |
使い分けのポイント
たわみの許容範囲
- たわみが許容値を超える場合は、両端支持梁を選定する方が有利です。
- 片持ち梁の場合、長さを短くするか断面を大きくするなどの補強が必要。
荷重の位置と種類
- 荷重が集中する場合は片持ち梁、均等に分布する場合は両端支持梁が適しています。
設計スペース
- 設置スペースが限られる場合、片持ち梁が有効。
- 両端支持梁は支持部を設けるスペースが必要。
メンテナンス性
- 自由端へのアクセスが必要な場合は片持ち梁が便利。
- 両端支持梁は均等荷重で安定性を重視する場面に適しています。
実際の設計例
片持ち梁の使用例
- ロボットのアーム: アームの先端で物をつかむ動作が多い場合に適用。
- 壁面看板: 壁から突き出して設置する場合、片持ち梁が理想的。
両端支持梁の使用例
- 橋梁設計: 両端支持梁にすることで均等荷重を実現し、長期間の耐久性を確保。
- 工作機械のベッドフレーム: 均等分布荷重で剛性を確保し、高精度の加工を実現。
トラブルを防ぐためのポイント
たわみの予測
許容たわみを設計時に明確にし、適切な梁形式を選択。
材料選定
梁の材質によるヤング率の違いがたわみに大きく影響します。
例: SS400とアルミ合金の比較。
補強の導入
必要に応じて梁の断面形状を変更（I型、H型など）することで、剛性を向上。
片持ち梁と両端支持梁は、それぞれ特性が異なり、用途に応じた選定が必要です。片持ち梁は自由端の操作性を重視する場面で有効であり、両端支持梁は均等荷重による安定性を確保する場面で効果を発揮します。設計段階でたわみや応力を正確に計算し、用途に応じた梁形式を選ぶことで、安全性と効率性を兼ね備えた設計が可能になります。
ヤング率と断面二次モーメントの役割
梁のたわみ計算には、材料のヤング率（E）と断面二次モーメント（I）が重要な役割を果たします。
ヤング率（E）
ヤング率は材料の硬さを示す指標で、値が大きいほど材料が硬く、変形しにくいことを意味します。機械設計において、使用する材料のヤング率を考慮することで、たわみを抑える設計が可能です。
例えば、鋼材（SS400）はヤング率が約205,000 N/mm²で、アルミニウム合金（A5052）の約70,000 N/mm²と比較して大きいため、同じ荷重条件下で鋼材の方がたわみが小さくなります。
断面二次モーメント（I）
断面二次モーメントは、梁の断面形状に依存し、形状が異なればたわみも変わります。一般に、断面積が大きく、形状が剛性のあるものであるほど、たわみは小さくなります。
断面二次モーメントの計算式は、断面形状に応じて異なりますが、以下は代表的な断面形状の場合の式です。
まとめ
梁のたわみ計算は、機械設計における安全性と効率性を左右する重要なプロセスです。ヤング率や断面二次モーメントなどの物理的特性を理解し、適切な計算を行うことで、無駄のない設計を実現できます。また、支持条件や荷重条件に応じた計算式を正確に使用することが、信頼性の高い機械設計には不可欠です。
不安があるポイントではたわみを計算して失敗のない設計を心がけましょう！
コメント