機械設計において、梁(はり)のたわみは
構造物や機械部品の設計において重要な要素です。
特に、たわみを小さく抑えることは、
強度や剛性の確保に直結し、設計の信頼性を向上させます。
たわみは材料のヤング率に加え、
断面形状の影響も大きく受けます。
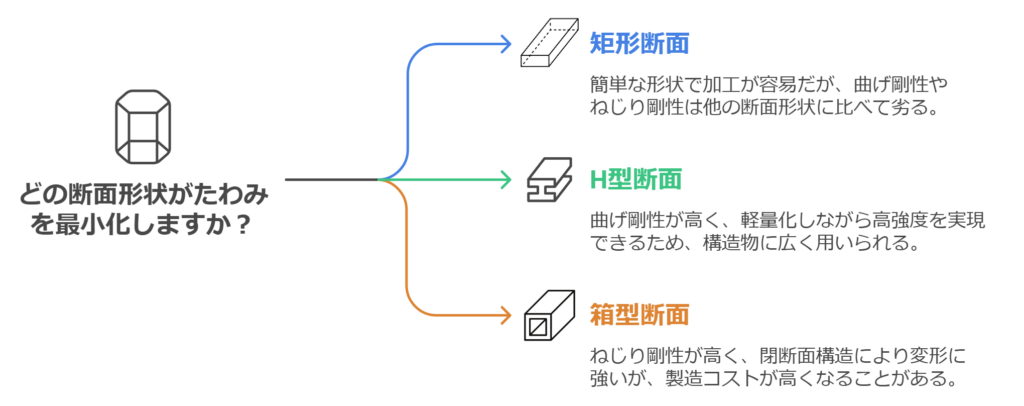
この記事では、矩形断面、H型断面、箱型断面の
3つの代表的な断面形状について、たわみの特性を比較し、
それぞれの断面形状がどのようにたわみに影響するかを解説します。
たわみと断面形状
はりに対するたわみは、主に次の要素によって決定されます。
荷重の大きさと分布
- 荷重が大きいほどたわみが増加します。
梁の長さ
- 梁が長くなるほどたわみが大きくなります。
材料のヤング率
- 材料の剛性を示し、ヤング率が高い材料ほどたわみが小さくなります。
断面二次モーメント(I)
- 断面形状に依存し、たわみを小さくするための重要な要素です。
- 断面二次モーメントが大きいほど、梁はたわみにくくなります。
この断面二次モーメント(I)は、断面形状と材料の配置に依存しており、
梁のたわみ量に直接影響します。
各断面形状の特徴
次に、各断面形状の基本的な特徴と断面二次モーメントの計算式を紹介します。
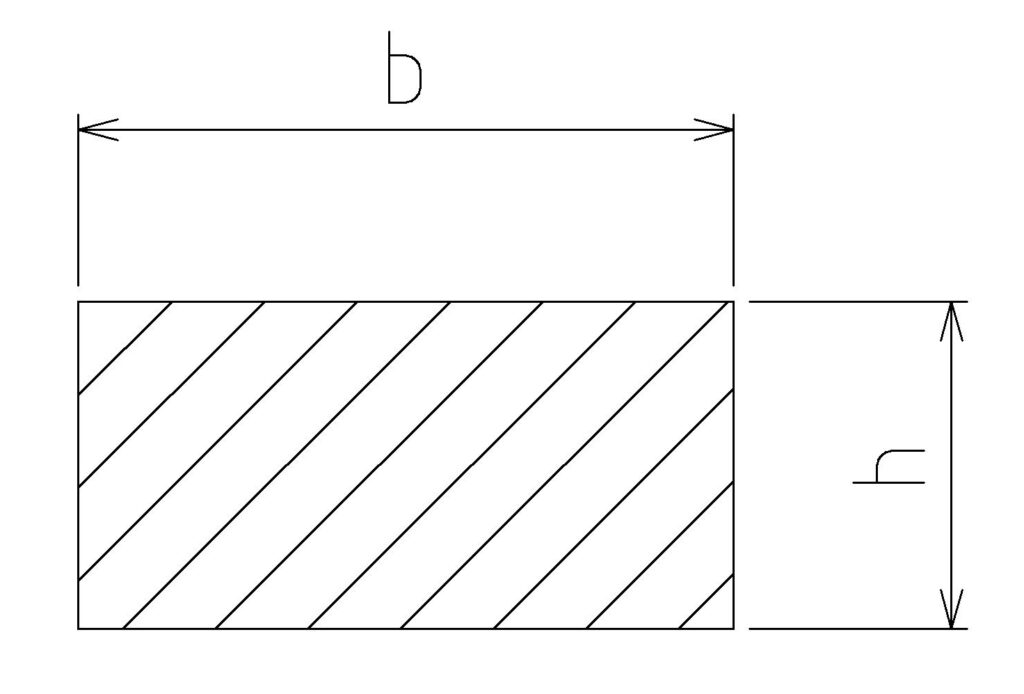
矩形断面
矩形断面は、もっともシンプルな形状で、
幅 b と高さ h からなる長方形の断面です。
この断面形状は多くの一般的な構造に使用されますが、
剛性を確保するには高さ h を大きくする必要があります。
断面2次モーメント(I)
\( \displaystyle I=\frac{bh^3} {12}\)
- b:断面の幅
- h:断面の高さ
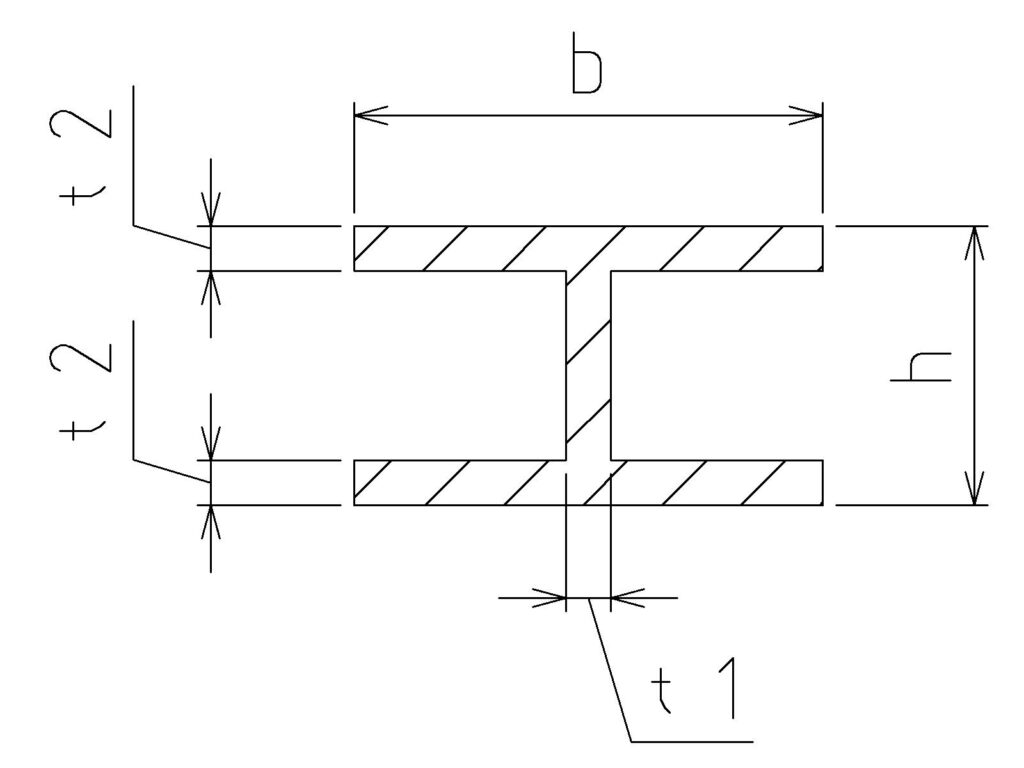
H型断面
H型断面は、梁や柱としてよく使用される断面形状で、
中央のウェブ(縦部)と、
上下に位置するフランジ(水平部)から構成されています。
フランジが外側に広がっているため、
断面二次モーメントを効率的に高めることができ、
少ない材料で高い剛性を実現します。
断面2次モーメント(I)
\( \displaystyle I=\frac{bh^3} {12}-\frac{(b-t1)(t2)^3} {12}\)
- b:フランジの幅
- h:断面の全高さ
- t1:ウェブの厚さ
- t2:フランジの厚さ
H型断面は材料を外側に配置することで、
少ない材料で大きな断面二次モーメントを得られるため、
軽量化と剛性のバランスが良好です。
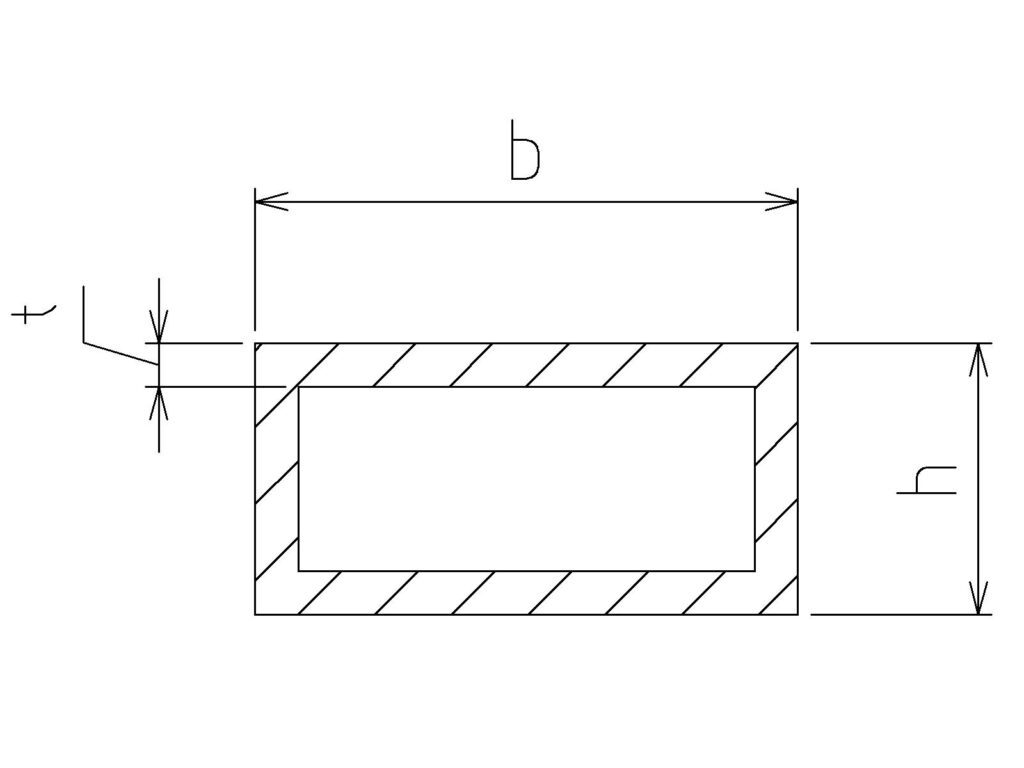
箱型断面
箱型断面(角パイプ)は、外周が四角形で内部が空洞の断面形状です。
外周部に材料が集中しているため、剛性を高く保ちながらも軽量化が可能です。
また、対称的な形状で曲げやねじりに対する強度が高いことも特徴です。
✅ 断面2次モーメント(I)
\( \displaystyle I=\frac{bh^3} {12}\)
- h:外部高さ
- b:外部幅
- t:壁厚
箱型断面は、H型断面と同様に外周部に材料を集中させることで、
大きな断面二次モーメントを持ちつつ、
内部が空洞であるため軽量化に優れています。
たわみの比較:矩形断面 vs H型断面 vs 箱型断面
3つの断面形状のたわみを、片持ち梁におけるたわみ計算式を使って比較します。
たわみは以下の式で求められます。
\( \displaystyle δ=\frac{FL^3} {3EI}\)
- δ:たわみ量(mm)
- F:荷重(N)
- L:梁の長さ(mm)
- E:材料のヤング率(N/mm²)
- I:断面二次モーメント(mm⁴)
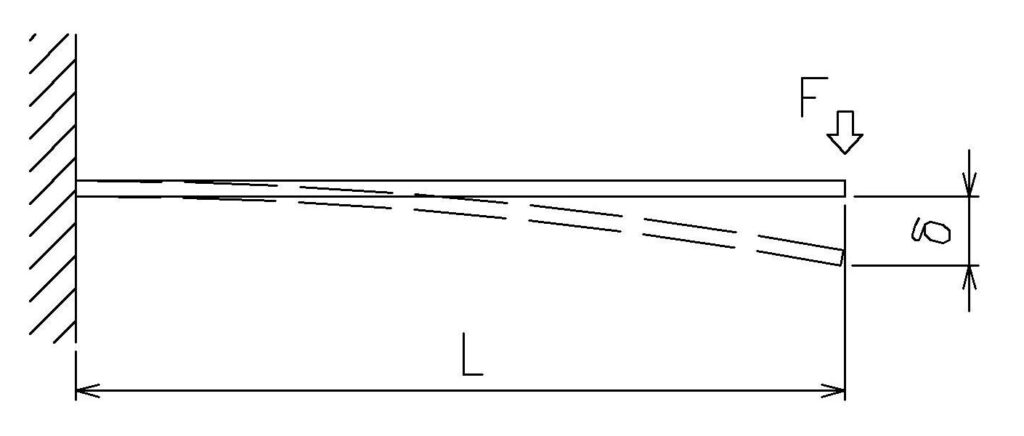
梁の条件設定
同一の荷重条件と材料を使用して、各断面形状のたわみを比較します。
- 梁の長さ L=1000 mm
- 荷重 F=100 N
- 材料のヤング率 E=205 GPa=205000Mpa(SS400の場合)
- 材料の密度 ρ=0.00000786kg/㎣ (SS400の場合)
- 各断面の幅は b=50 mm
- 断面積は500㎟とし質量を同一する

材料の幅と断面積を同一とし、
形状の違いでどの程度たわみに差がでるか計算していきます。
各断面形状の断面二次モーメント
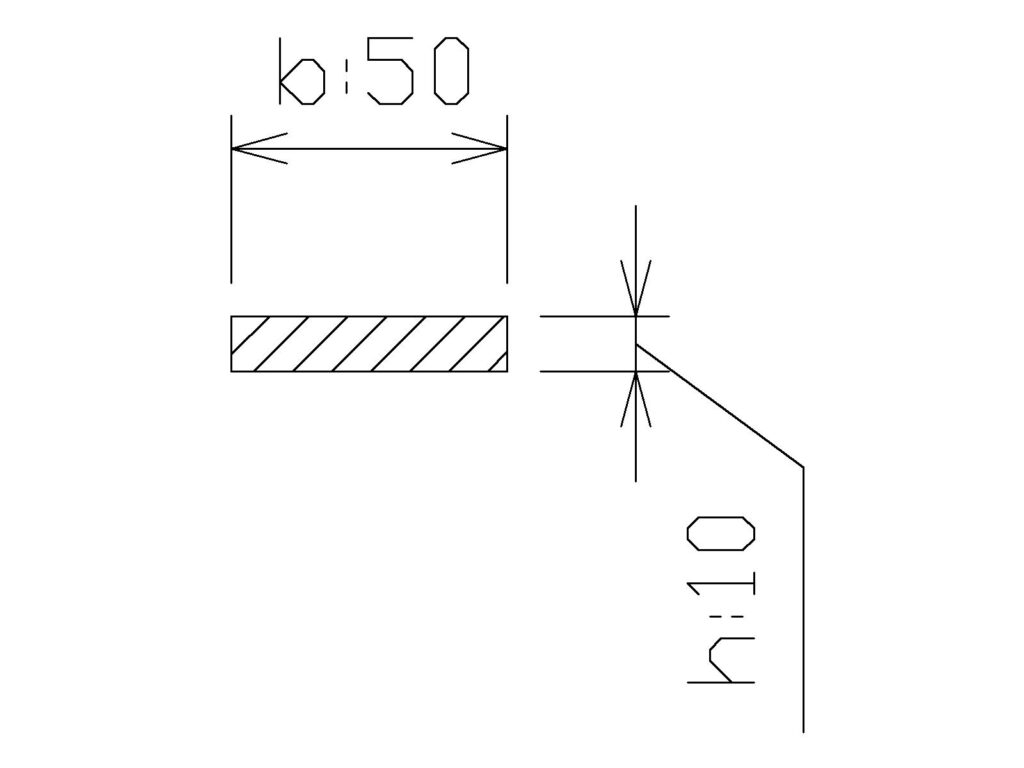
矩形断面
断面積
\( \displaystyle 50×10=500㎟\)
断面二次モーメント
\( \displaystyle I=\frac{50×10^3} {12}\)
\( \displaystyle I=4166.7\)
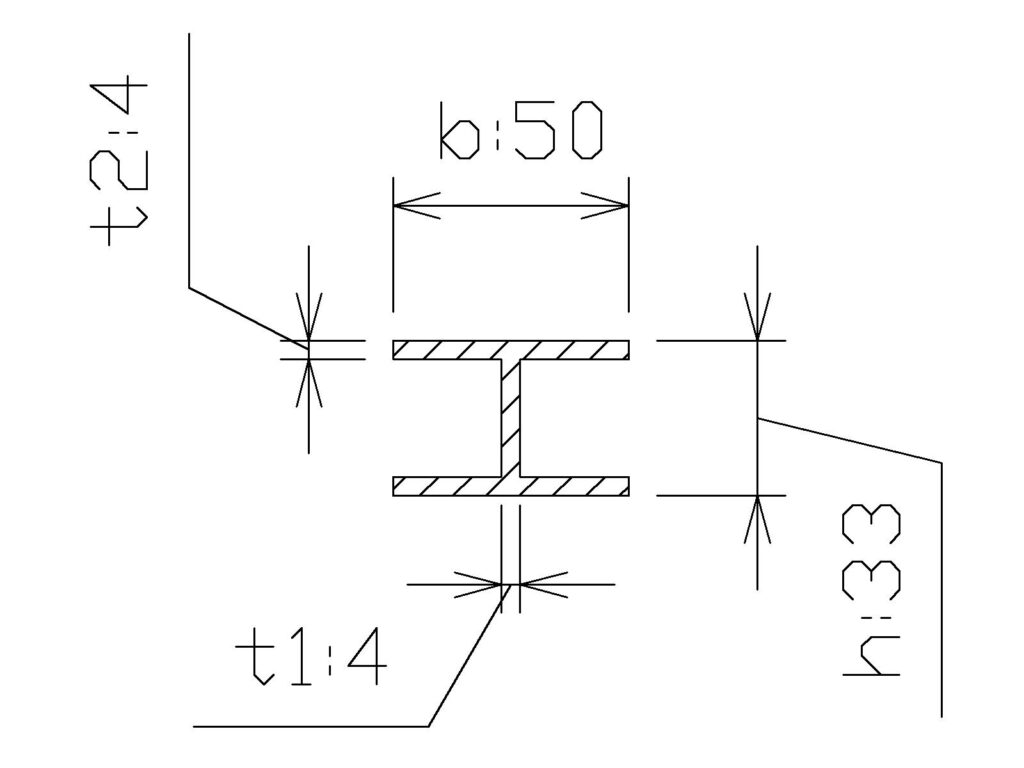
H型断面
断面積
\( \displaystyle 2×50×4+(33-4-4)×4=500㎟\)
断面2次モーメント
\( \displaystyle I=\frac{50×33^3-(50-4)×25^3} {12}\)
\( \displaystyle I=89841.7\)
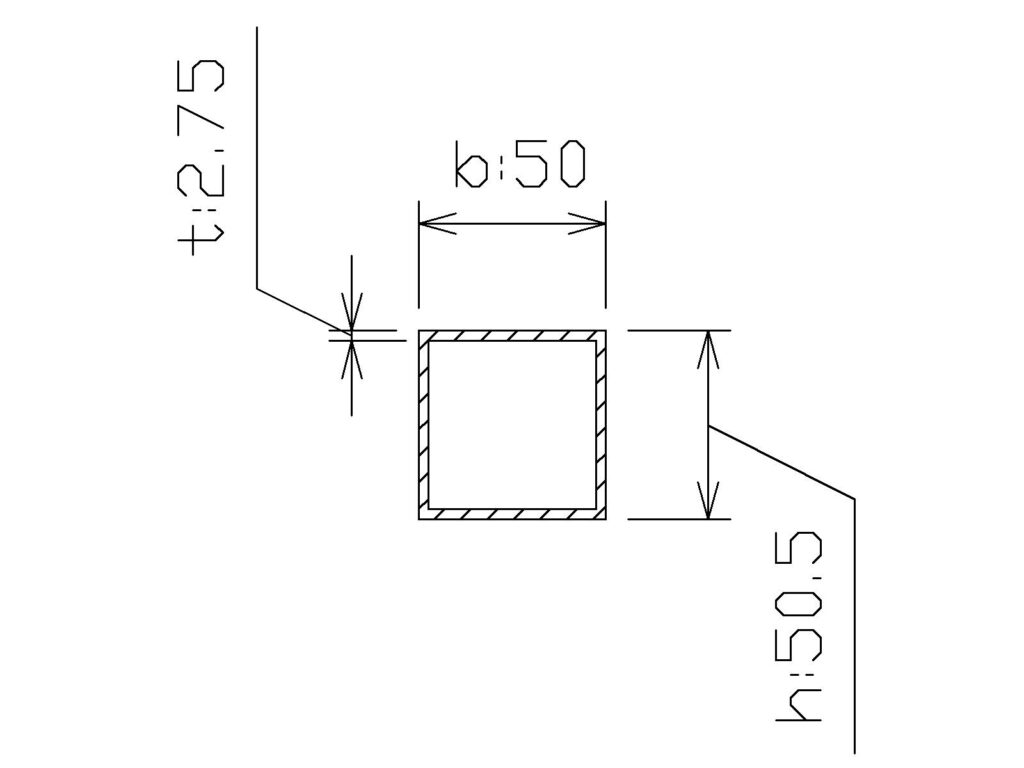
箱型断面(角パイプ)
断面積
\( \displaystyle 50×50.5-45×45=500㎟\)
断面2次モーメント
\( \displaystyle I=\frac{(50×50.5^3-45×45^3)} {12}\)
\( \displaystyle I=194896.4\)
たわみ量の比較
上記の条件で計算すると、たわみ量は以下の通りです。
矩形断面
\( \displaystyle δ=\frac{100×1000^3} {3×205000×4166.7}\)
\( \displaystyle δ=39.02mm\)
\( \displaystyle δw=\frac{wL^4} {8EI}\)
\( \displaystyle w=密度(kg/㎣)×断面積(㎟)×g(9.8)\)
\( \displaystyle w=7.86×10^-6(kg/㎣)×50×10(㎟)×g(9.8)=0.0385\)
\( \displaystyle δw=\frac{0.0385×1000^4} {8×205000×4166.7}\)
\( \displaystyle δw=5.63mm\)
\( \displaystyle δ=39.02mm+5.63mm\)
\( \displaystyle δ=44.65mm\)
H型断面
\( \displaystyle δ=\frac{100×1000^3} {3×205000×89841.7}\)
\( \displaystyle δ=1.81mm\)
\( \displaystyle δw=\frac{wL^4} {8EI}\)
\( \displaystyle w=密度(kg/㎣)×断面積(㎟)×g(9.8)\)
\( \displaystyle w=7.86×10^-6(kg/㎣)×50×10(㎟)×g(9.8)=0.0385\)
\( \displaystyle δw=\frac{0.0385×1000^4} {8×205000×89841.7}\)
\( \displaystyle δw=0.26mm\)
\( \displaystyle δ=1.81mm+0.26mm\)
\( \displaystyle δ=2.07mm\)
箱型断面(角パイプ)
\( \displaystyle δ=\frac{100×1000^3} {3×205000×194896.4}\)
\( \displaystyle δ=0.83mm\)
\( \displaystyle δw=\frac{wL^4} {8EI}\)
\( \displaystyle w=密度(kg/㎣)×断面積(㎟)×g(9.8)\)
\( \displaystyle w=7.86×10^-6(kg/㎣)×50×10(㎟)×g(9.8)=0.0385\)
\( \displaystyle δw=\frac{0.0385×1000^4} {8×205000×194896.4}\)
\( \displaystyle δw=0.12mm\)
\( \displaystyle δ=0.83mm+0.12mm\)
\( \displaystyle δ=0.95mm\)
たわみ比較の結果
| 断面形状 | 断面2次モーメント | 総たわみ |
| 矩形断面 | 4166.7 | 44.65mm |
| H型断面 | 89841.7 | 2.07mm |
| 箱型断面 | 194896.4 | 0.95mm |

断面形状の違いでたわみ数値にかなりの差がでることがわかります。
機械設計をする上で材質選定だけでなく、形状の選定も重要です。
それぞれの形状の長所と短所を理解し、最適な設計を心がけよう!
断面形状ごとの特性比較
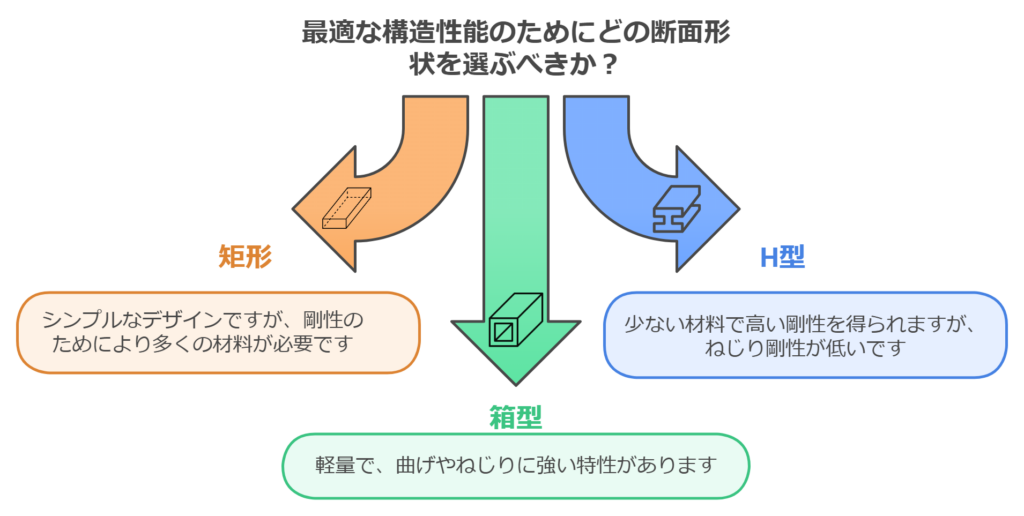
矩形断面はシンプルな形状で、
剛性を確保するには高さを増やす必要があります。
フランジやウェブがないため、
他の形状に比べて効率的に材料を使っているとは言えません。
H型断面は、少ない材料で高い剛性を得られるため、
重量を抑えつつ剛性を高くする設計に適しています。
ただし、ねじり剛性が低いことがあるため、注意が必要です。
箱型断面は、内部が空洞であるため軽量化が可能で、
対称性により曲げやねじりに強い特性があります。
剛性を高めたいが、重量を抑えたい場合に有効です。
まとめ
機械設計におけるたわみを考慮した断面形状の選定は、設計の重要な要素です。
矩形断面、H型断面、箱型断面の特性を理解し、
用途に応じて最適な形状を選定することで、
効率的かつ信頼性の高い設計を実現できます。
それぞれの形状の長所と短所を把握し、
荷重条件やコスト、重量などを考慮した上で、適切な断面を選びましょう。


















コメント