機械設計において、三角関数は非常に重要な役割を果たします。
特に、直線と角度を扱う設計作業では、
三角関数の知識が欠かせません。
三角関数は、機械部品の設計や解析において、
角度、距離、力の関係を正確に計算するために用いられます。
この知識が不足していると、設計精度が低下し、
機械全体の性能や耐久性に悪影響を及ぼすことがあります。
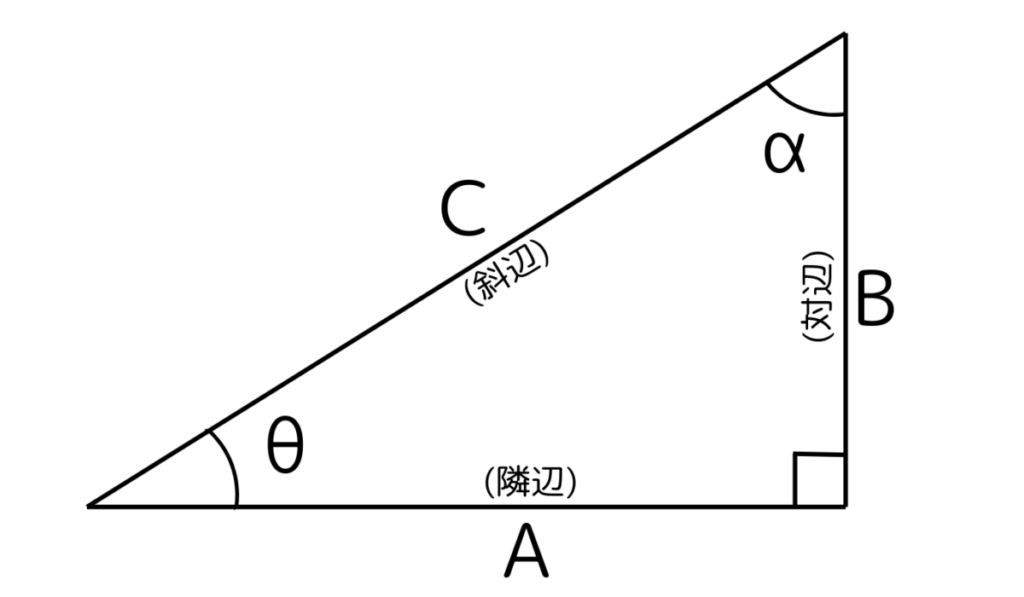
- 2辺の長さが分かっている
- 1辺と角度がわかっている
三角関数の基本概念
三角関数には主に
「サイン(sin)」
「コサイン(cos)」
「タンジェント(tan)」
があります。
これらは直角三角形の角度と辺の長さの比を表し、
角度や長さの計算に使用されます。
特に、回転運動や傾斜が関係する機械部品の設計において、
これらの関数が必要となります。
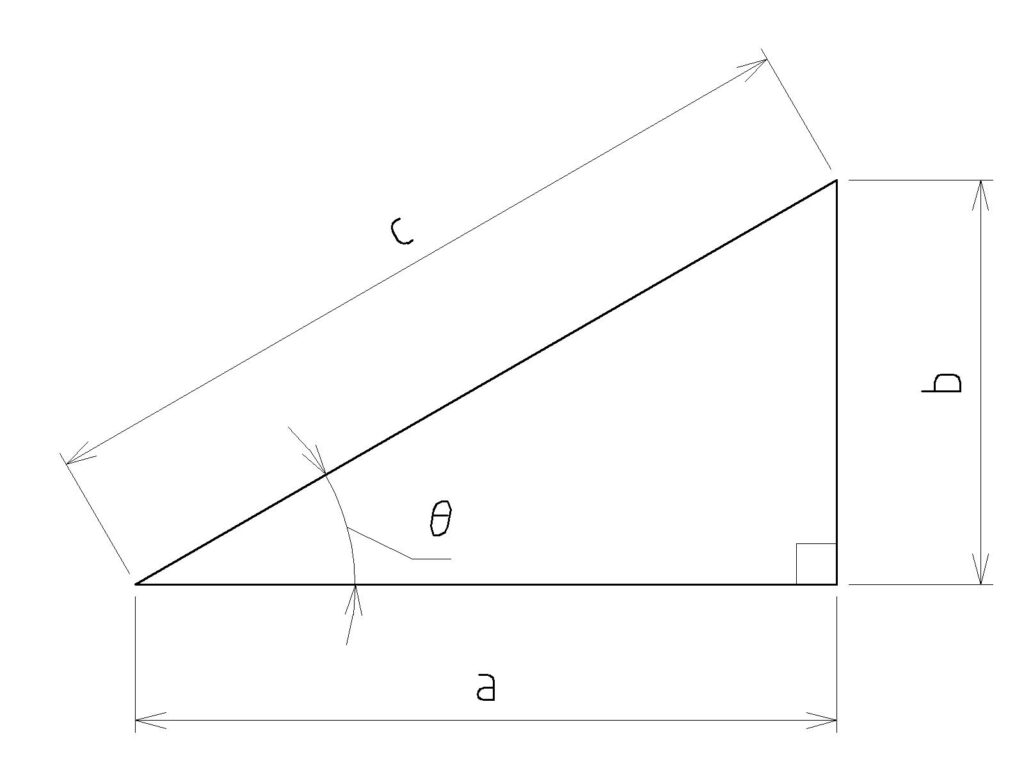
サイン(sin):対辺/斜辺
\( \displaystyle sinθ=\frac{b} {c}\)
コサイン(cos): 隣辺 / 斜辺
\( \displaystyle cosθ=\frac{a} {c}\)
タンジェント(tan):対辺 / 隣辺
\( \displaystyle tanθ=\frac{b} {a}\)
三角関数値の一覧
| 角度 (θ) | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|
| 30° | \( \displaystyle \frac{1} {2}=0.5\) | \( \displaystyle \frac{√3} {2}≈0.866\) | \( \displaystyle \frac{1} {√3}≈0.577\) |
| 45° | \( \displaystyle \frac{1} {√2}≈0.707\) | \( \displaystyle \frac{1} {√2}≈0.707\) | \( \displaystyle 1\) |
| 60° | \( \displaystyle \frac{√3} {2}≈0.866\) | \( \displaystyle \frac{1} {2}=0.5\) | \( \displaystyle √3≈1.732\) |
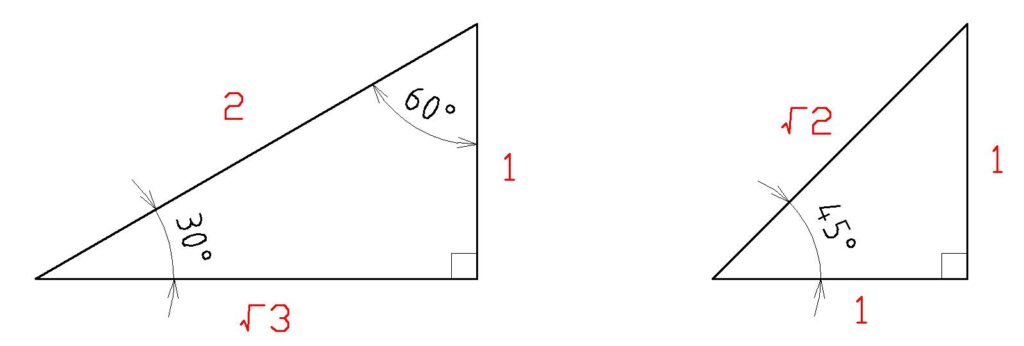

設計段階では概算を行うことも重要です。
よく使われる値を暗記しておくと便利です。
三角関数が必要な理由
機械設計では、機構がさまざまな角度で動作したり、
力が異なる方向に作用することがあります。
これらの複雑な状況を正確に把握し、
最適な設計を行うためには、
三角関数を活用して角度や長さ、
力の分解を行うことが必要です。
以下に、三角関数がどのように機械設計で
活用されているかを具体的に説明します。
応用例 1: 斜面上の力の分解
状況設定
- 物体の質量: m=10 kg
- 斜面の角度: θ=30°
- 重力加速度: g=9.8 m/s2
斜面上に置かれた物体に働く力を、以下のように分解。
- 垂直方向の力 (F垂直)
斜面に対して垂直に働く力 - 水平方向の力 (F水平)
斜面に沿って物体を下に引っ張る力
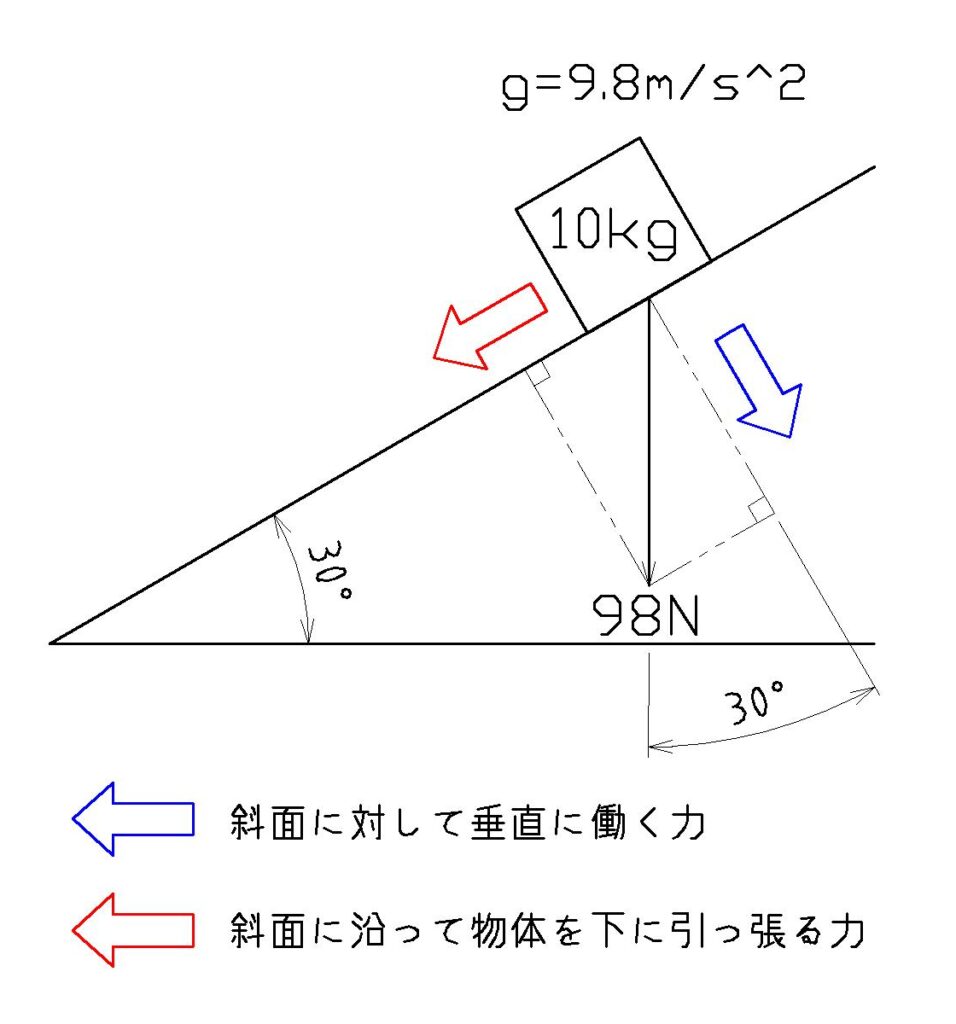
計算式
F垂直=m⋅g⋅cos(θ)
F水平=m⋅g⋅sin(θ)
計算
F垂直=10⋅9.8⋅cos(30°)
F水平=10⋅9.8⋅sin(30°)
数値解
- cos(30°)≈0.866
- sin(30°)=0.5
F垂直=10⋅9.8⋅0.866=84.868 N
F水平=10⋅9.8⋅0.5=49.0 N

三角関数を活用するにあたって直角三角形を探すことが重要です。
さまざまな計算に応用できるので上手に活用しましょう。
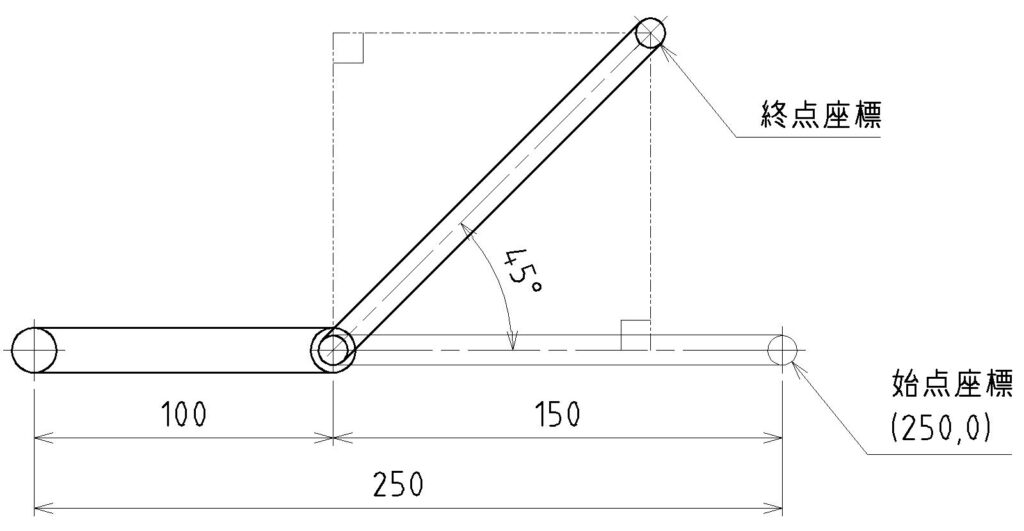
応用例 2: リンク機構の終点座標の計算
状況設定
リンク機構において、リンクの長さと回転角度から終点座標を計算します。
- 固定リンクの長さ (a): 100 mm
- 可動リンクの長さ (b): 150 mm
- 回転角度 (θ): 45°
計算式
リンクの終点座標 (x, y) は以下で求められます:
x=a+b⋅cos(θ)
y=b⋅sin(θ)
計算
x=100+150⋅cos(45°)
y = 150⋅sin(45°)
数値解
- cos(45°)≈0.707
- sin(45°)≈0.707
x=100+150⋅0.707=100+106.05=206.05 mm
y=150⋅0.707=106.05 mm
リンク機構の終点座標は、以下のようになります
(x,y)=(206.05,106.05) mm

このように三角関数では角度、距離、力の関係を正確に計算することができます。
これらの計算を正確に行うことで、設計の精度が向上させましょう。
三角関数を活用した応用例
1. クランク機構
クランク機構は、回転運動を直線運動に変換するための機構であり、
その動作は三角関数を使って計算できます。
クランクの回転角度に応じて、
ピストンの直線移動距離が変化します。
このとき、三角関数を使うことで、
回転角度と移動距離の関係を正確に計算できます。
2. カム機構
カム機構も同様に、回転運動から直線運動を得る仕組みですが、
その輪郭形状やフォロワーの動きを計算する際には、
三角関数が不可欠です。
カムの回転角度とフォロワーの上下運動の関係は、
カムの設計段階で三角関数を使って詳細に計算されます。
3. ベルトやチェーン駆動のテンション解析
ベルトやチェーン駆動では、ベルトの張力やチェーンのたわみを解析する際に、
斜め方向に作用する力を水平方向および垂直方向に分解する必要があります。
ここでも三角関数が活用され、各方向の力の大きさを計算します。
注意点と推奨点
計算精度
- 三角関数を使用する際、小数点以下の精度を適切に設定することが重要です。
- 精度が不足すると、設計における寸法や力の計算に誤差が生じます。
使用ツールの確認
- 設計ソフトや電卓では、ラジアンと度数法の違いに注意が必要です。
- 多くのミスは、これらの単位を誤った状態で計算を進めることで発生します。
学習の継続
- 三角関数の計算に慣れるためには、日常的な訓練が必要です。
- リンク機構や斜面の力学的な問題を解くことで、自然と身に付けることができます。
まとめ
三角関数は機械設計において、力の分解や合成、回転運動の解析、
カムやクランク機構の動作解析など、多くの場面で不可欠です。
これらの計算を正確に行うことで、設計の精度が向上し、
機械全体の性能や耐久性が高まります。
特に、複雑な角度や力が絡む設計作業では、
三角関数の理解と応用が必要です。
機械設計者として、三角関数をしっかりと習得することは、
より精密で効率的な設計を行うための重要なステップとなるでしょう。






















コメント