機械設計を学ぶ上で、「応力（おうりょく）」という言葉はとても重要です。応力とは、物体に外力が加わったとき、材料内部に発生する力のことを指します。適切な設計をするためには、どのような応力が発生するのかを理解することが不可欠です。
本記事では、初心者の方にもわかりやすく、「応力」の基本を解説していきます！
応力とは？
✅ 応力とは、「物体に力が加わったときに、内部で発生する抵抗の力」です。
✅ イメージとしては、スポンジを両側から引っ張ると、中で力がかかっている状態になります。
この内部の力が「応力」です。
- 応力の単位は「Pa（パスカル）」または「N/mm²」で表されます。
- これは1mm²あたりにどれくらいの力が加わっているかを示します。
応力の弾性限界・降伏点・破断をわかりやすく解説
機械設計では、材料がどれくらいの力に耐えられるのかを知ることが重要です。そのために、「弾性限界」「降伏点」「破断」の概念を理解しておく必要があります。
本項では、それぞれの違いや関係性を初心者でもわかるように解説します！
弾性変形と塑性変形（そせいへんけい）
応力が大きくなると、材料は変形しますが、変形の仕方には元に戻る変形（弾性変形）と、元に戻らない変形（塑性変形）があります。
材料が壊れるまでの流れは、以下のようになります。
1️⃣ 弾性限界（Elastic Limit）
2️⃣ 降伏点（Yield Point）
3️⃣ 破断（Fracture）
弾性限界
弾性限界とは、材料が元に戻れる限界の応力のことです。
🔍 たとえ話
✔ ゴムを軽く引っ張ると、手を離したときに元の形に戻ります。
✔ しかし、強く引っ張りすぎると、伸びたまま戻らなくなります。
この「元に戻れるギリギリのライン」が弾性限界です。
✅ 弾性限界以下の力 → 材料は元に戻る（弾性変形）
✅ 弾性限界を超える力 → 材料は元に戻らなくなる（塑性変形）
📌 設計でのポイント
機械設計では、部品が長期間使われることを考え、通常は弾性限界を超えない範囲で設計します。
降伏点
降伏点とは、材料が一気に変形し始める応力のことです。
🔍 たとえ話
✔ クリップを少し曲げると、手を離せば元に戻ります。
✔ しかし、ある程度以上曲げると、元に戻らずグニャっと変形します。
この「変形が始まるポイント」が降伏点です。
✅ 降伏点以上の力が加わると、材料は元に戻らない。
✅ 降伏点を超えた後は、比較的少ない力でも変形し続ける。
📌 設計でのポイント
降伏点を超えないように設計しないと、部品が変形してしまい、機械としての機能が損なわれる可能性があります。
破断
破断とは、材料が完全に壊れることです。
🔍 たとえ話
✔ クリップを何度も曲げ伸ばしすると、最後にはポキッと折れます。
✔ この「折れる瞬間」が破断です。
✅ 材料には「引張強さ（破断強さ）」があり、それを超えると破断する。
✅ 降伏点を超えて変形が進み、最終的に耐えられなくなると破断する。
📌 設計でのポイント
・通常、材料が破断するような応力がかからないように設計します。
・しかし、安全装置や切断部品など、一部の設計では意図的に破断を利用することもあります。
弾性限界・降伏点・破断の関係まとめ
| 状態 | 応力の範囲 | 変形の種類 | 変形後の状態 |
|---|---|---|---|
| 弾性変形 | 弾性限界以下 | 弾性変形 | 元に戻る |
| 塑性変形 | 降伏点以上 | 塑性変形 | 変形したまま |
| 破断 | 引張強さを超える | 破壊 | 材料が壊れる |
🔹 弾性限界 → 材料が元に戻れるギリギリの応力。
🔹 降伏点 → 材料が変形し始めるポイント。
🔹 破断 → 材料が壊れる瞬間。
機械設計では、弾性限界や降伏点を考慮して安全な設計をすることが重要です！
これらの概念を理解し、適切な材料選定・設計を行いましょう！
応力の種類
機械設計では、以下の5つの応力が特に重要です。
引張応力（Tensile Stress）
物体を引っ張る力によって発生する応力。
✅ 例: ワイヤーやボルトが引っ張られるとき
✅ 特徴: 材料が伸びて破断する可能性がある
圧縮応力（Compressive Stress）
物体を押しつぶす力によって発生する応力。
✅ 例: 建物の柱、ボールベアリングの内輪
✅ 特徴: 材料が短くなり、座屈（折れ曲がる現象）が発生する可能性
せん断応力（Shear Stress）
物体をずらすような力によって発生する応力。
✅ 例: はさみで紙を切るとき、ボルトやリベットが受ける力
✅ 特徴: 材料が横方向にずれて破壊される
ねじり応力（Torsional Stress）
物体をねじる力によって発生する応力。
✅ 例: ドライブシャフト、ボルトの締結部
✅ 特徴: ねじれによる破壊が起こる可能性
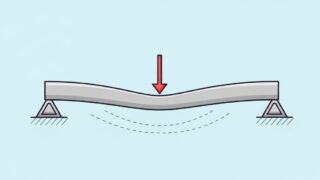
曲げ応力（Bending Stress）
物体を曲げる力によって発生する応力。
✅ 例: 梁（はり）、スプリング
✅ 特徴: 一方は引張、もう一方は圧縮の状態になる
応力の計算方法をわかりやすく解説
機械設計では、「応力（おうりょく）」を計算することがとても重要です。応力を正しく求めることで、部品が壊れず、安全に機能する設計ができます。
本項では、初心者でもわかりやすいように「応力の計算方法」について解説します！
引張応力・圧縮応力の計算式
引張や圧縮の応力は、以下の式で求められます。
\( \displaystyle σ=\frac{F} {A}\)
✅ σ（シグマ） = 応力（N/mm²）
✅ F = 加わる力（N）
✅ A = 力がかかる断面積（mm²）
🔍計算例
直径10mmの円柱に1,000Nの引張力が加わる場合、応力を求めます。
1. 断面積を求める
\( \displaystyle A=\frac{πd^2} {4}=\frac{3.14×10^2} {4}=78.5㎟\)
2. 応力を求める
\( \displaystyleσ=\frac{1000} {78.5}=12.7N/㎟\)
せん断応力の計算式
せん断（横ずれ）の応力は、以下の式で求められます。
\( \displaystyle τ=\frac{F} {A}\)
✅ τ（タウ） = せん断応力（N/mm²）
✅ F = 加わるせん断力（N）
✅ A = せん断が発生する面積（mm²）
🔍計算例
直径8mmのボルトに500Nのせん断力が加わる場合、せん断応力を求めます。
1. 断面積を求める
\( \displaystyle A=\frac{πd^2} {4}=\frac{3.14×8^2} {4}=50.24㎟\)
2. せん断応力を求める
\( \displaystyle σ=\frac{500} {50.24}=9.95N/㎟\)
ねじり応力の計算式
ねじりの応力は、以下の式で求めます。
\( \displaystyle τ=\frac{Tr} {J}\)
✅ τ（タウ） = ねじり応力（N/mm²）
✅ T = ねじりモーメント（N·mm）
✅ r = 半径（mm）
✅ J = 極断面二次モーメント（mm⁴）
Jの計算は形状によって異なりますが、円柱の場合は以下の式を使います。
\( \displaystyle J=\frac{πd^4} {32}\)
曲げ応力の計算式
曲げの応力は、以下の式で求めます。
\( \displaystyle σ=\frac{My} {I}\)
✅ M = 曲げモーメント（N·mm）
✅ y = 中心からの距離（mm）
✅ I = 断面二次モーメント（mm⁴）
Iの計算は形状によって異なりますが、長方形の断面の場合は以下の式を使います。
\( \displaystyle I=\frac{bh^3} {12}\)
✅ b = 幅（mm）
✅ h = 高さ（mm）
応力は、「力 ÷ 面積」で求めるのが基本で、種類ごとに計算式が変わります。
機械設計では、応力を正しく計算し、適切な材料や形状を選ぶことが重要です。
まずは、引張・圧縮・せん断の基本計算を理解し、ねじりや曲げ応力も少しずつ学んでいきましょう！
応力を考慮した設計のポイント
✅ 材料選びが重要
👉 材料によって、応力に対する強度が異なります。
（🔍例：鉄は引張強度が高いが、せん断には弱い）
✅ 形状を工夫しよう！
👉 部品の形状によって、応力の集中を防ぐことができます。
（🔍例：角を丸くすることで応力集中を減らす）
✅ 安全率を考慮する！
👉 必要な強度よりも余裕を持たせた設計が重要。
（🔍例：突然の衝撃にも耐えられるようにする）
まとめ
「応力」は機械設計の基礎となる考え方で、強度や耐久性を決める大事な要素です。設計の際には、どのような応力が発生するのかをしっかり理解し、適切な材料や形状を選ぶことが重要になります！
これから機械設計を学ぶ方も、まずは「引張」「圧縮」「せん断」「ねじり」「曲げ」の5つの応力をしっかり押さえておきましょう！
コメント