機械設計において「速度」や「加速度・減速度（加減速度）」は、設計の根幹を支える非常に重要な物理量です。これらを正しく理解することで、モーターやアクチュエーターの選定、機構の剛性設計、制御設計などに大きな差が出ます。
この記事では、機械設計の初心者にもわかりやすいように、速度と加減速度の基礎から、設計での活用ポイント、注意点までを丁寧に解説します。
速度とは？～位置変化の速さ～
速度の定義
速度とは、「物体の位置がどれだけ速く変化するか」を表す量で、単位は m/min（メートル毎分） や mm/s（ミリメートル毎秒） がよく使われます。
たとえば、あるコンベアが10秒で5m移動した場合、
速度は、 5m ÷ 10s = 0.5 m/s となります。
機械設計での速度の例
- ベルトコンベアの搬送速度
- スライダーやリニアガイドの移動速度
- モーターの回転速度（角速度）など
速度はただ速ければ良いわけではなく、製品の精度や安全性、騒音、寿命に影響するため、目的に応じた適切な速度設定が必要です。
加減速度とは？～速度変化の速さ～
加速度と減速度の違い
加速度は「速度がどれだけ速くなるか」、減速度は「速度がどれだけ速く落ちるか」という、速度の変化量を表す値です。
- 単位は m/s²（メートル毎秒毎秒） や mm/s²（ミリメートル毎秒毎秒）
- 正の値 → 加速
- 負の値 → 減速
機械設計での加減速度の例
- ロボットアームが急停止したときの加速度
- モーターが起動・停止する際の加減速カーブ
- 位置決め制御でのS字加減速（スムーズな動きのための制御手法）
加減速度の計算式
\( \displaystyle a（加減速度）=\frac{Vmax} {t}\)
初心者向け！速度と加減速度の計算例
あるステージが0.2秒で100mm移動するとします。
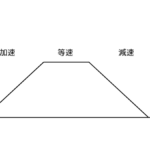
加減速の時間がそれぞれ0.05秒ずつ、等加速度運動と仮定します。
平均速度
\( \displaystyle \frac{移動距離} {加速＋等速＋減速時間}=\frac{100} {0.05+0.1+0.05}=500mm/s\)
最高速度
「加減速が等加速度運動」であることを前提として、以下のステップで最大速度（Vmax）を求めます。
ステップ①：各区間の移動距離を求める
✅ 加速区間（0 → Vmax、時間 0.05秒）
等加速度運動の移動距離は下記の式で求めます。
\( \displaystyle x=\frac{1} {2}at^2\)
- aは加速度
- tは時間
\( \displaystyle a（加速度）=\frac{Vmax} {t} なので、\)
\( \displaystyle x(加速)=\frac{1} {2}・\frac{Vmax} {t}・t^2=\frac{1} {2}Vmax・t\)
\( \displaystyle x(加速)=\frac{1} {2}Vmax・0.05\)
✅ 減速区間も同様（対称なので）
\( \displaystyle x(減速)=\frac{1} {2}Vmax・0.05\)
✅ 等速区間（時間 0.1秒）
\( \displaystyle x(等速)=Vmax・0.1\)
ステップ②：全体の距離を合計する
\( \displaystyle x(合計)=x（加速)+x(等速)+x(減速)\)
\( \displaystyle x=\frac{1} {2}Vmax・0.05+Vmax・0.1+\frac{1} {2}Vmax・0.05\)
\( \displaystyle x=Vmax・(0.025+0.1+0.025)=Vmax・0.15\)
ステップ③：移動距離 100mm を代入して解く
\( \displaystyle 100=Vmax・0.15\)
\( \displaystyle Vmax=\frac{100} {0.15}=666.67mm/s\)
加速度・減速度
\( \displaystyle a（加減速度）=\frac{Vmax} {t}=\frac{666.67} {0.05}=13,333.4mm/s^2\)
結論
✅ 平均速度：500mm/s
✅ 最高速度：666.67mm/s
✅ 加減速度：13，333.4ｍｍ/ｓ2
平均速度と最高速度の違いを考慮することが重要
とくにロボットやリニア搬送装置などでは、加減速の設計が命です！
平均速度だけで考えると、モーターの性能が足りなくなるリスクがある。
実際の機械では「最大速度」や「加速度」に合わせた設計が必要。
速度と加減速度を考慮した設計が重要な理由
剛性と振動の対策
加速度が大きいと、慣性力も大きくなり、構造物にたわみや振動が発生します。
これにより、位置ズレや繰り返し精度の悪化を引き起こします。
🔍 対策例
- 加速度を抑える
- 軽量部品を使用
- 高剛性設計を行う
モーター・アクチュエーターの選定
モーター選定では「必要なトルク」＝「負荷の質量×加速度×半径」から求められます。
したがって加減速度を見誤ると、モーターの能力不足や過剰スペックによるコスト増に繋がります。
安全性と耐久性
高速かつ高加速度での運転は、ブレーキ距離が伸びたり、摩耗が激しくなったりして、安全性や寿命にも影響します。
注意点と推奨ポイント
🚫 注意点
- 加速度を高くしすぎると衝撃が増し、機械寿命が短くなる
- サーボモーターやアクチュエーターの制御性能の限界を超えないこと
- 制御機器側の設定（加減速時間、S字制御）との整合性を確認すること
✅ 推奨ポイント
- 移動時間から逆算して加速度を設定する
- 構造物の剛性や振動特性を考慮した上で速度と加減速度を決定する
- シミュレーションやプロファイル設計（速度プロファイル）を活用する
加減速度の表し方:「s(秒）」と「g」の違いをわかりやすく解説！
機械設計や装置設計に関わっていると、「加減速度：0.1ｓ」とか「加減速度：0.3g」という表記に出会うことがあります。
でも、
「どっちの表記が正しいの？」
「そもそも何が違うの？」
と混乱してしまう方も多いはずです。本項では、そんな初心者の方向けに、加減速度の2つの表記方法とその違い、使い分け、注意点をやさしく解説していきます！
そもそも「加減速度」とは？
「加減速度」とは、物体が加速・減速にかかる速さ（勢い）のことです。
たとえば、モーターでステージを動かすときに、いきなり1000mm/sでは動けません。少しずつ速度を上げる「加速」、止まる直前にはゆるやかに速度を落とす「減速」が必要になります。
「どのくらいの早さで加速・減速するか」を表すのが、加減速度という指標です。
加減速度の2つの表記方法
時間で表す（単位：秒）
🔍 例
- 加減速度：0.1秒(0.1s)
- これは、「最大速度に達するまでに0.1秒かかる」という意味です。
- つまり、加速時間・減速時間をそのまま表しています。
📌 よく使われる場面
- タクトタイムが重要な搬送装置
- 動作シミュレーション
- モーターのモーションプロファイル
加速度で表す（単位：g）
🔍 例
- 加速度：0.3g
- この「g」は重力加速度（9.8m/s²）を基準にしています。
- つまり、0.3g = 0.3 × 9.8 = 約2.94m/s² の加速度です。
これは、「単位時間あたりにどのくらい速度が変化するか」を意味しています。
📌 よく使われる場面
- ロボットやアクチュエーターのスペック表
- 製品仕様書
- 振動・衝撃解析などの物理評価
具体例で比較しよう！
あるステージが、最大速度500mm/s（=0.5m/s）に達するまでの「加減速度の違い」を見てみましょう。
【ケース①】加減速度：0.1秒（秒表記）
- 最大速度：0.5m/s
- 加速時間：0.1秒
→ このときの加速度は？
\( \displaystyle a（加減速度）=\frac{Vmax} {t}\)
\( \displaystyle a（加減速度）=\frac{0.5} {0.1}=5.0m/s^2\)
🔍 g換算すると…
\( \displaystyle 5÷9.8＝約0.51ｇ\)
【ケース②】加速度：0.3g（g表記）
- 加速度：0.3g ≒ 2.94 m/s²
- 最大速度：0.5m/s
→ このときの加速時間は？
\( \displaystyle t=\frac{v} {a}=\frac{0.5} {2.94}=0.17秒\)
表記の違いまとめ
| 表記 | 意味 | 利点 | 欠点 |
|---|---|---|---|
| s（秒） | 何秒で加速/減速するか | 感覚的にわかりやすい | 装置ごとに条件が変わる |
| g（重力加速度） | 加速度の強さ | 定量評価ができる | 慣れないとイメージしにくい |
注意点と設計でのポイント
🚫 表記の「単位」を見落とさない！
- 「0.1」と書いてあっても、それが秒なのか、gなのかでまったく意味が変わります。
- 必ず「単位が明示されているか」を確認しましょう。
🚫 装置の性質に合った表記を使う！
- 装置の可動範囲や安全性の管理が重要な場合は「g」での制御が適している
- 逆に、タクト管理や動作時間の調整が重要なら「秒」ベースの表記が有利
🚫 g表記には加速度リミットに注意！
- 高加速度（例：3.2g）を設定すると、部品への衝撃や振動、破損のリスクが高まります。
- リニアガイドやステージのスペック上限を超えないように、カタログ値や実測値を確認することが大切です。
推奨：変換式を活用しよう！
どちらの表記も一長一短あるため、必要に応じて変換して使い分けるのがおすすめです。
時間（t）→ 加速度（a）
\( \displaystyle a=\frac{v} {t}\)
加速度（a）→ 時間（t）
\( \displaystyle t=\frac{v} {a}\)
最大速度 v がわかれば、自由に行き来できます！
✅ 加減速度には「秒（s）で表す方法」と「g（重力加速度）で表す方法」がある
✅ 秒表記は時間管理に便利、g表記は物理的な加速度管理に便利
✅ 単位の見間違いや使い分けには注意が必要
✅ 設計では変換式を使って、適切な加速度を設定しよう！
初心者のうちは、「秒ベース」の表記から慣れていくと感覚がつかみやすいです。
でも、いずれ「g」表記にも慣れておくと、他社との仕様比較やトラブルシューティングにも強くなります！
まとめ：速度と加減速度の理解は設計品質のカギ
速度や加減速度は一見単純な物理量に見えますが、設計の基礎から精度・寿命・コストまで幅広く影響します。特に初心者のうちは、モーターや装置が動く様子ばかりを重視しがちですが、裏ではこうした数値のバランスがとても大切です。
最初は「どのくらいの速度で動かすべきか？」「加速度を大きくしたら何が起きるか？」という視点を持つだけでも、より良い機械設計に近づきます。
コメント