重心とは、物体全体の質量が集中していると考えられる点のことです。
機械設計において、重心の位置は、部品の動作や安定性、負荷分布、
さらには振動や騒音の制御に大きな影響を及ぼします。
本記事では、重心の重要性とその設計における考慮ポイントについて解説します。
重心の計算をわかりやすく解説
重心の計算は、部品や機械全体の「バランス」を理解するための基本的な手法です。
難しい数式を扱う前に、イメージしやすい例を通じて解説します。
重心とは?
重心は、物体全体の質量が「一点に集中している」と考えられる点です。
例えば、シーソーに物を載せるとき、バランスが取れる位置が「重心」に相当します。
身近な例で考える重心
一本の棒の重心を考える
均一な棒(例えば竹の棒)を手に持って水平に保つとします。
棒の長さが均等で密度も均一なら、重心は「真ん中」にあります。
棒を1本の指で支える場合、真ん中を支えるとバランスが取れます。
重りが付いた棒の重心を考える
棒の片方に重りをつけると、重心は真ん中から重りがある側にずれます。
バランスを取るには、重心がずれた位置で棒を支える必要があります。
重心の計算方法
重心の計算は、物体を「小さな質量の集まり」と考え、
それぞれの位置と質量をもとに計算します。
以下は基本的な計算の考え方です。
部品の重心位置を計算するためには、
質量の分布と部品形状を考慮する必要があります。
以下に一般的な計算式を示します。
質量重心の計算式
\( \displaystyle xc=\frac{Σ(xi・mi)} {Σmi} ,yc=\frac{Σ(yi・mi)} {Σmi} ,zc=\frac{Σ(zi・mi)} {Σmi}\)
- xc,yc,zcは重心座標
- xi,yi,ziは各質量要素の座標
- miは各質量要素の質量
部品が均一な密度の場合
部品が均一な密度で構成されている場合、
重心は幾何学的な中心に一致します。
単純な1次元の例
物体A(3kg)はx=0の位置にあり、物体B(5kg)はx=10の位置にあるとします。
重心の位置xcを計算する公式
\( \displaystyle xc=\frac{(mA・xA)+(mB・xB)} {mA+mB}\)
mA:物体Aの質量(3kg)
xA :物体Aの位置(x=0)
mB:物体Bの質量(5kg)
xB :物体Bの位置(x=10)
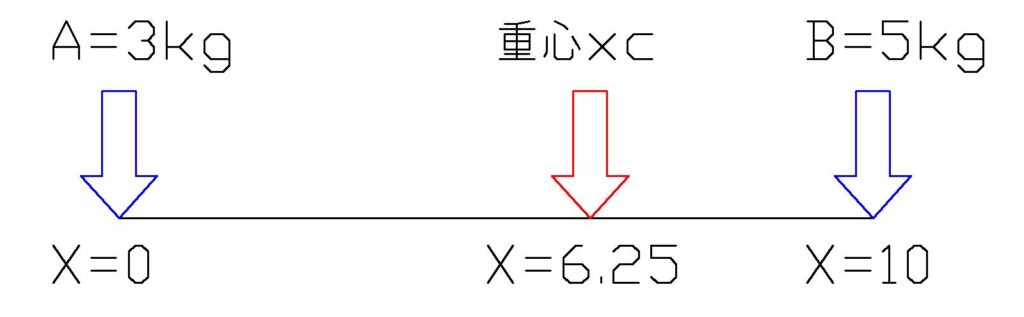
計算すると
\( \displaystyle xc=\frac{(3・0)+(5・10)} {3+5}=\frac{(0)+(50)} {8}=6.25\)
結果:重心はx=6.25の位置にあります。
平面(2次元)の例:プレートの重心を求める
問題設定
- 縦長の長方形プレートに小さい四角形の穴が空いているとします。
- 長方形のプレートは100mm × 50mm(厚さ均一で面積の中心に重心あり)。
- 小さい四角形の穴は30mm × 20mmで、プレートの左上から(10mm, 10mm)に位置します。
- プレートの密度は均一です。
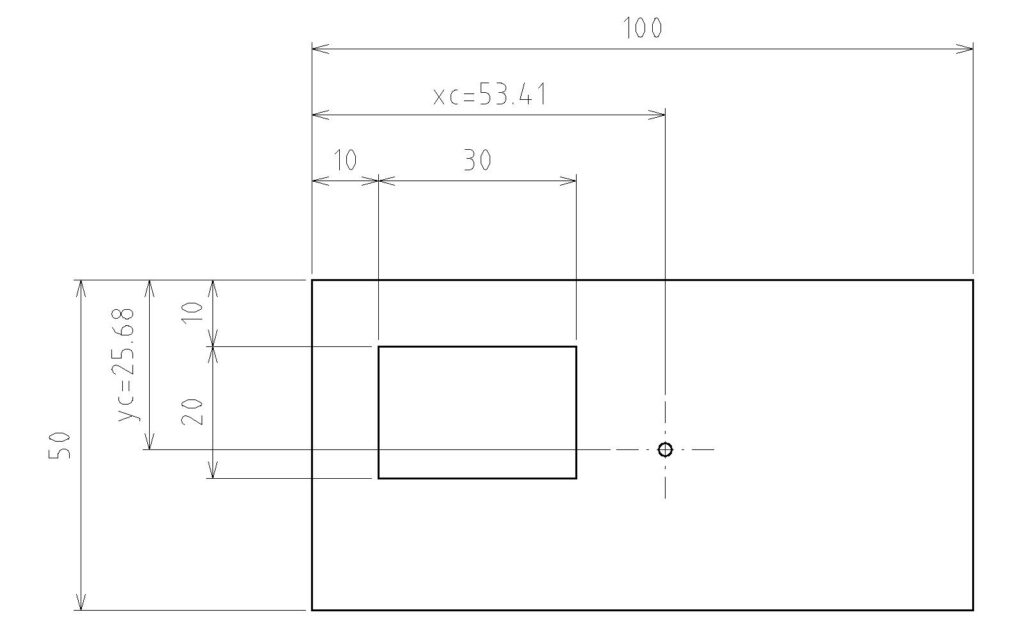
計算の考え方
重心を求めるには、穴を「負の面積」として扱い、全体の重心を計算します。
各部の重心を特定する
プレート全体の重心(穴がない場合)
\( \displaystyle (xp,yp)=(50,25)\)
穴の重心(左上隅からの位置)
\( \displaystyle (xh,yh)=(10+\frac{30} {2}),(10+\frac{20} {2})=(25,20)\)
各部の面積を計算
プレートの面積
\( \displaystyle Ap=100×50=5000㎟\)
穴の面積
\( \displaystyle Ah=30×20=600㎟\)
全体の重心を計算
重心の公式
\( \displaystyle xc=\frac{Σ(Ai・xi)} {ΣAi},yc=\frac{Σ(Ai・yi)} {ΣAi}\)
xcの計算
\( \displaystyle xc=\frac{(5000・50)-(600・25)} {5000-600}≈53.41mm\)
ycの計算
\( \displaystyle yc=\frac{(5000・25)-(600・20)} {5000-600}≈25.68mm\)
結果
プレート全体の重心
\( \displaystyle (xc,yc)≈(53.41mm,25.68mm)\)
実際の設計で重心を求める手順
- 形状を分割する
- 部品全体を、簡単な形状(例えば四角形や円柱)に分割します。
- 各部分の質量と中心位置を計算する
- 各部分の質量を計算し、幾何学的中心の位置を記録します。
- 重心公式を使う
- 質量と位置を公式に当てはめて、全体の重心位置を計算します。
CADソフトで重心を求める方法
設計段階では、2Dや3DのCADソフトを使用することで、
重心の位置を簡単に確認できます。
重心設計のポイント
- 均一な密度を想定
- 計算が簡単になるため、部品が均一な密度であると仮定します。
- 補正を考慮
- 実際の部品では材料の不均一性や加工精度の影響で、
計算通りの重心位置にならない場合があります。
- 実際の部品では材料の不均一性や加工精度の影響で、
- バランス調整
- 重心がずれると性能に影響を及ぼすため、
必要に応じてカウンターウェイトなどで調整します。
- 重心がずれると性能に影響を及ぼすため、
重心の計算は、機械設計において部品の安定性や
効率を向上させるための基本技術です。
設計の初期段階で重心を正確に把握し、
必要に応じてバランス調整を行うことで、
より高性能で安全な機械設計を実現できます。
部品設計における重心の重要性
安定性の向上
機械全体や部品の重心位置が適切に
設計されていると、機械が安定して動作します。
高速回転部品や移動する部品では、
重心位置がずれることで振動が発生し、
動作が不安定になる可能性があります。
負荷分布の均等化
重心位置が適切であると、
機械の各部分にかかる負荷が均等になります。
これにより、過剰な応力が特定の部位に
集中することを防ぎ、部品の寿命を延ばすことができます。
効率的な動力伝達
重心の位置が適切に設計されていると、
動力伝達の効率が向上します。
特に回転部品では、重心が軸心と一致していないと
バランスが崩れ、エネルギーロスが発生します。
安全性の向上
重心の位置が安定することで、
設備や機械の転倒や部品の落下などの事故を防ぐことができます。
重心の計算と設計への反映
設計における配慮
部品の形状や質量を調整し、
重心位置を設計の意図に合わせて最適化します。
重心が設計上の基準位置から大きくずれた場合は、
カウンターウェイトの追加や形状変更を検討します。
設計ソフトウェア(CAD)を活用して、
重心位置を視覚的に確認しながら設計することも有効です。
重心設計の応用事例
ロボットアーム
ロボットアームの重心位置を適切に設定することで、
モーターの負荷を均一化し、省エネルギー化や動作精度の向上を実現します。
回転体(ホイールやローター)
重心位置がずれるとバランスが崩れ、
振動や騒音の原因となります。
バランスウェイトを取り付けることで、
重心位置を補正することが一般的です。
構造物の安定性
大型設備やフレームの設計では、
重心を低くすることで転倒リスクを軽減します。
特に可搬型の設備では、
重心位置の低下が安全性の確保に寄与します。
重心設計における注意点
材料の不均一性
実際の部品では、材質の不均一性が原因で
計算通りの重心位置にならない場合があります。
そのため、実機での測定を行うことが推奨されます。
振動解析の実施
回転部品や移動部品の場合、
重心位置が振動特性に大きく影響します。
重心を考慮した設計だけでなく、
振動解析も並行して行いましょう。
製造誤差の考慮
加工精度や組み立て精度が重心位置に影響する場合があるため、
必要に応じて補正が可能な設計を取り入れます。
まとめ
部品の重心位置を適切に設計することは、
機械の性能や安全性を大きく左右する重要な要素です。
設計段階で重心位置を考慮し、
質量分布を最適化することで、
効率的で安定した機械設計が可能になります。
「重心」を意識した設計を行い、
設備の信頼性と長寿命化を目指しましょう!

















コメント