機械設計を学び始めると必ず出てくるのが
「力の合成」と「力の分解」です。
例えば、ボルトや部品にかかる力を正しく理解しなければ、
強度不足による破損や設計ミスにつながります。
✔ 力の合成(複数の力をまとめる)
複数の力が作用するときに、それを1つの「合力」として表す方法。
✔ 力の分解(1つの力を分ける)
ある力を、基準となる方向に沿った成分に分けて考える方法。
この2つを理解することで、
複雑な力の問題もシンプルに考えられるようになります。
自動計算フォーム~力の合成と分解~
力の合成
力の分解①(水平と垂直)
力の分解②(傾斜のある力の分解)
力の合成の基本
同一直線上の力の合成
最も簡単なケースは、同じ直線上にかかる力の合成です。
🔍 例)
10 N の力と 15 N の力が同じ向きに作用 → 合力は 25 N
10 N と 15 N が逆向きに作用 → 合力は 5 N(大きい方の方向)
👉 機械設計では、ベルトやチェーンの張力、ボルトの軸力などでよく出てきます。
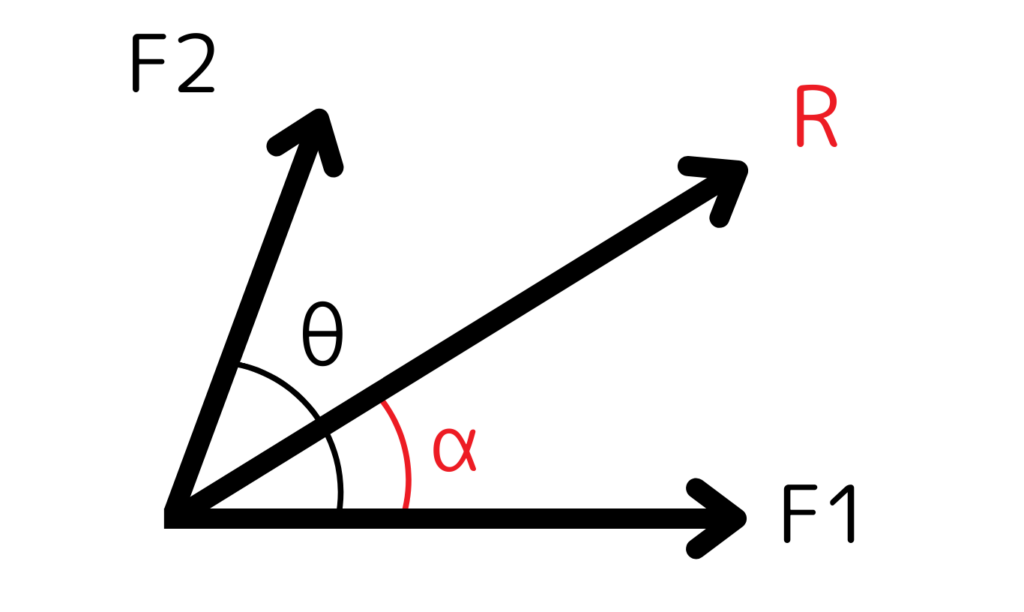
角度のある力の合成(平行四辺形の法則)
2つの力が角度を持って働くときは「平行四辺形の法則」を使います。
合力の大きさは以下で求められます。
\( \displaystyle R=\sqrt{F_1^2 + F_2^2 + 2F_1F_2 \cos \theta}\)
ここで、
- R:合力(Resultant force)
- F1,F2:それぞれの力の大きさ
- θ:力の間の角度
また、合力の向きは以下で表せます。
\( \displaystyle tan \alpha = \frac{F_2 \sin \theta}{F_1 + F_2 \cos \theta}\)

上記、自動計算フォーム(力の合成)の入力式になります。
具体例:2つの力の合成
ある物体に対して、次の2つの力が同時に作用しています。
- 水平方向に 100 N の力(F1)
- それに対して 60° の角度で、80 N の力(F2)が斜め上向きに作用している
🔧 設定条件
| 項目 | 内容 | 計算フォームの値 【力の合成】 |
|---|---|---|
| 荷重の大きさ F1 | F1 = 100 N | 100 |
| 荷重の大きさ F2 | F2 = 80 N | 80 |
| 荷重の方向 θ | 水平(F1)に対して 60° | 60 |
このとき、2つの力を合成して、合力の大きさと向きを求めると…
合力の大きさ
\( \displaystyle R=\sqrt{F_1^2 + F_2^2 + 2F_1F_2 \cos \theta}\)
\( \displaystyle R=\sqrt{100^2 + 80^2 + 2×100×80× \cos 60°}\)
\( \displaystyle R=\sqrt{10000 + 6400 + 8000}\)
\( \displaystyle R=\sqrt{24400}≈156.205\)
合力の向き(水平からの角度 α)
\( \displaystyle tan \alpha = \frac{F_2 \sin \theta}{F_1 + F_2 \cos \theta}\)
\( \displaystyle tan \alpha = \frac{80 \sin 60°}{100 + 80 \cos 60°}\)
\( \displaystyle tan \alpha = \frac{69.282032303}{140}=0.49487166\)
\( \displaystyle α = arctan(0.49487166)≈26.330°\)
物体には約 156.205 N の力が、水平から 26.330° 上向きの方向に働いていることになります。
つまり、2つの力を合わせると、より強い力が斜め方向に作用しているということです。
力の分解の基本
力の分解の基本式
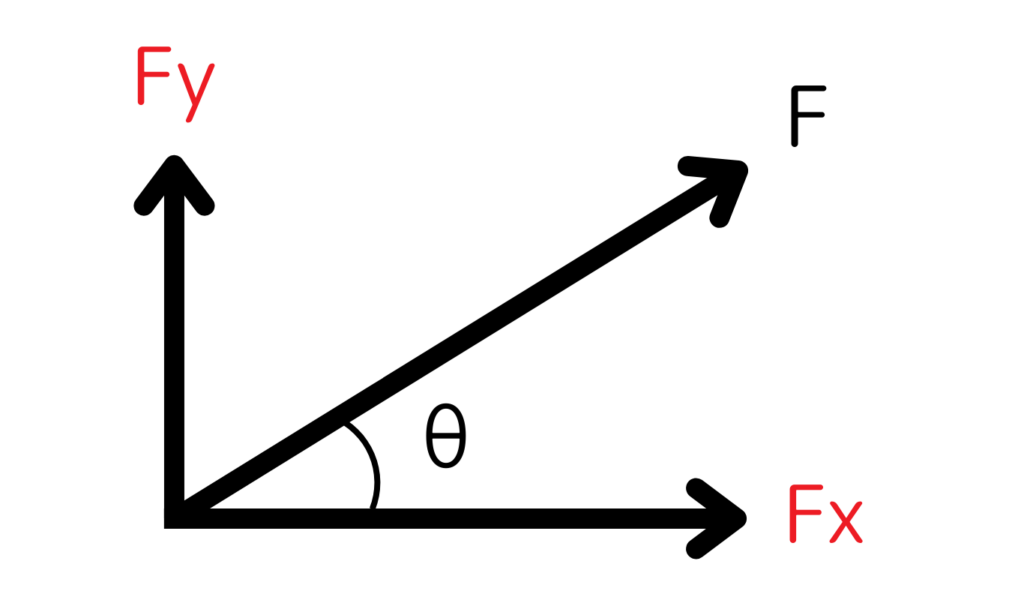
1つの力 F を、基準となる2方向に分ける場合
\( \displaystyle F_x = Fcosθ\)
\( \displaystyle F_y = Fsinθ\)

これが「分力」の考え方です。
上記、自動計算フォーム(力の分解①)の入力式になります。
具体例①:2つの力の分解(水平と垂直)
例題:斜めに引っ張る力
100 N の力でロープを水平に対して 30° 上向きに引いた場合、水平成分と垂直成分を求める。
🔧 設定条件
| 項目 | 内容 | 計算フォームの値 【力の分解①】 |
|---|---|---|
| 荷重の大きさ F | F = 100 N | 100 |
| 荷重の方向 θ | 水平に対して 30° | 30 |
水平方向
\( \displaystyle F_x = Fcosθ\)
\( \displaystyle F_x = 100×cos30°\)
\( \displaystyle F_x ≈86.6N \)
垂直方向
\( \displaystyle F_y = Fsinθ\)
\( \displaystyle F_y = 100×sin30°\)
\( \displaystyle F_y = 50N\)
このとき、ロープが水平に支えるのは 86.6 N、持ち上げる方向に働くのは 50 N という意味です。
具体例②:2つの力の分解(傾斜のある力の分解)
傾斜45°のガイドレールに垂直荷重がかかる場合
ある機械装置において、ガイドレールが水平面に対して
45度の角度で傾斜して取り付けられている。
このガイドレール上に搭載された部品に対して、
重力による垂直下向きの荷重が100N作用している。
設計者は、この荷重を「ガイドレールの進行方向(レール軸方向)」と
「レールに垂直な方向(支持方向)」に分解し、
それぞれの力成分を算出する必要がある。
🔧 設定条件
| 項目 | 内容 | 計算フォームの値 【力の分解②】 |
|---|---|---|
| 荷重の大きさ F | F = 100 N | 100 |
| 荷重の方向 θ | 垂直下向き(重力方向) | 270 |
| 座標系(F1) α | F1:レール方向 | 225 |
| 座標系(F2) β | F2:レールに垂直な方向 | 315 |
🧮 分解の考え方
荷重Fは垂直方向(鉛直)に作用していますが、
ガイドレールが45°傾いているため、
この荷重を「レール方向(X軸)」と
「レールに垂直な方向(Y軸)」に分解します。
- 荷重方向 θ = 270°(真下)
- レール方向 α = 225°(F1)
- レール垂直方向 β = 315°(F2)
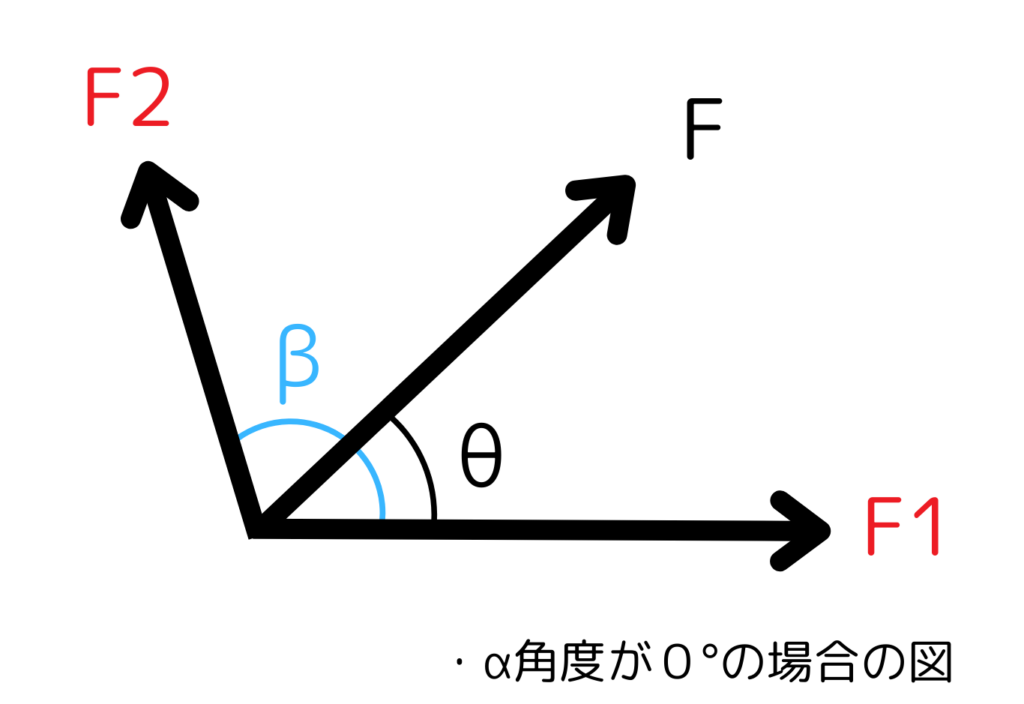
分解式(傾斜のある力の分解)
ある力 F が、ある方向(角度 \theta)に向かって作用しているとします。
この力を、任意の2方向(たとえばF1方向とF2方向)に分けたい場合、それぞれの方向がどの角度にあるかを指定する必要があります。
ここでは、F1方向が角度α、Y方向が角度β にあるとします。
このとき、力の分解は以下のように行います。
F1方向の成分
「力の向き」と「F1方向の向き」の角度差を使って、
\( \displaystyle F1 = F×cos(θ-α)\)
つまり、力がF1方向にどれだけ寄与しているかを計算します。
\( \displaystyle F1 = 100×cos(270-225)\)
\( \displaystyle F1 = 100×cos(45)\)
\( \displaystyle F1 ≈70.7N\)
F2方向の成分
同様に、F2方向との角度差を使って、
\( \displaystyle F2 = F×cos(θ-β)\)
F2方向への寄与を求めます。
\( \displaystyle F2 = 100×cos(270-315)\)
\( \displaystyle F2 = 100×cos(-45)\)
\( \displaystyle F1 ≈70.7N\)
解釈と設計への応用
| 成分 | 意味 | 設計での使い方 |
|---|---|---|
| F1(70.7 N) | レール方向の成分(滑ろうとする力) | 摩擦力の計算、駆動力の検討 |
| F2(70.7 N) | レールに垂直な成分(押し付ける力) | ガイドの支持力、変形・接触圧の評価 |
機械設計での具体的な利用シーン
ボルトやピンの設計
斜めの力を受けるボルトでは、
軸方向の引張力と横方向のせん断力に分解して評価します。
軸力が大きければ引張強度を確認し、
横方向が大きければせん断破壊を防ぐ設計が必要です。
クレーンや吊り具の設計
ワイヤーロープを角度をつけて吊る場合、
ロープの張力は重さ以上に大きくなります。
分解を正しく行わないと、
強度不足で破断事故につながります。
荷重分担を誤解して「1/2 で済む」と考えると大事故の原因になります。
リンク機構やカム機構
複雑な動きをする機械要素では、
各部材にかかる力を分解して解析しなければ
正しい寸法や材質を選べません。
注意点・設計者が陥りやすいミス
初心者への推奨ポイント
まとめ
「力の合成と分解」は、機械設計の基礎中の基礎でありながら、
実務に直結する重要な考え方です。
✔ 合成 → 複数の力をまとめて考える
✔ 分解 → 1つの力を成分に分けて考える
これを理解すると、荷重計算、強度設計、
安全設計などの幅広い場面で役立ちます。
記事冒頭にある「自動計算フォーム」を活用すれば、
実際に数値を入力して理解を深められます。
ぜひ手を動かしながら、力の基本を身につけてください。


















コメント