「なんで橋や鉄塔に三角形が多いの?」
橋、クレーン、鉄塔、さらには航空機の構造体など――
世の中のあらゆる構造物に
「三角形を組み合わせた形」が
多く使われていることに気づいたことはありませんか?
これは偶然ではなく、
「三角形」という形が構造力学的に
とても安定していて、壊れにくいからです。
この三角形を組み合わせて
構成された構造のことを「トラス構造」といいます。
この記事では、機械設計の基礎知識として
「なぜ三角形=トラス構造が強いのか?」を、
初心者にもわかりやすく解説します。
トラス構造とは?
まず「トラス構造」について簡単に説明します。
🔧 トラス構造の定義
トラス構造とは、細い部材(棒状部材)を三角形に組み合わせた構造体のこと。
各部材は「圧縮」または「引張」の力のみを受け持ち、
曲げモーメントは基本的に考慮しません。
よく見るトラス構造の例

見たことのあるものばかりですね。
ではなぜこの「三角形の連続」がこんなにも使われるのでしょうか?
なぜ三角形が強いのか?~構造的安定性の話~
結論から言うと、三角形は形が変形しにくい、
もっとも安定した平面図形だからです。
四角形と三角形を比較してみよう
四角形の場合
たとえば、木の棒を4本つなげて四角形を作ったとします。
その四角形の一角を押すとどうなるでしょう?
簡単に「ひしゃげて菱形」になってしまいますよね。
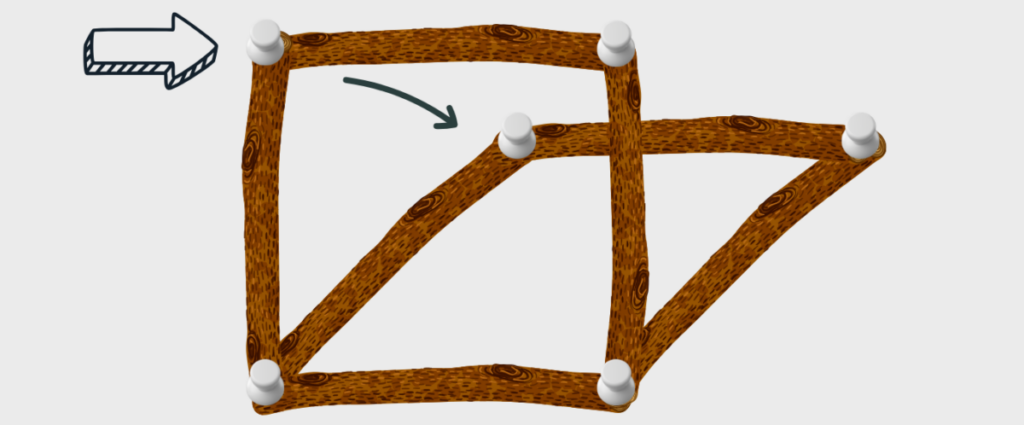

つまり、四角形は外力を受けると形が変わってしまう=不安定なんです。
三角形の場合
次に、3本の棒を使って三角形を作ります。
その一角を押しても、三角形はほとんど形が変わりません。
力を受けても、その力が部材に「分散」されて、変形せずに支えようとするのです。
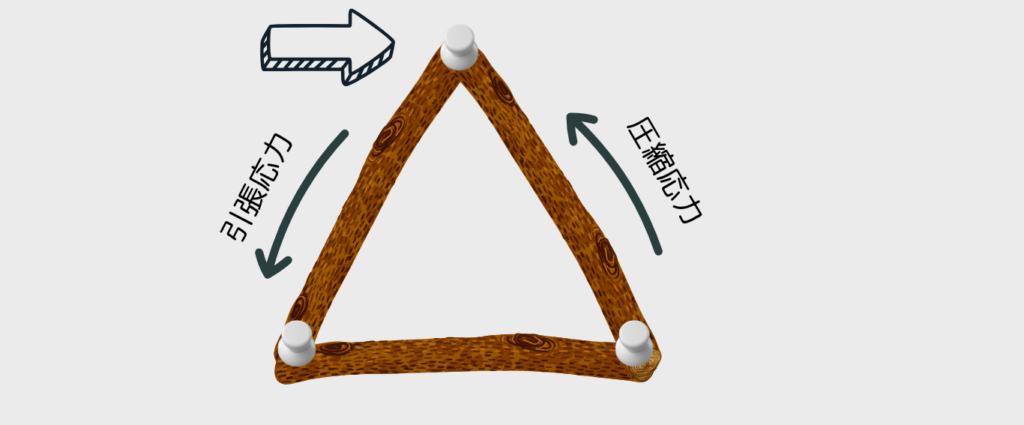

これが、三角形の構造的な強さの理由です。
力の流れを考える|「引張」と「圧縮」の使い分け
トラス構造が強い理由のもうひとつが、
力を「引張」か「圧縮」のどちらかだけで処理する点にあります。
引張と圧縮の違いとは?
| 種類 | 説明 | 構造への影響 |
|---|---|---|
| 引張力 | 部材を引っ張る力 | 材料の延びを考慮(破断注意) |
| 圧縮力 | 部材を押しつぶす力 | 座屈(くの字に折れる)に注意 |
トラス構造の特徴
トラスは三角形によって構成され、
各部材には曲げモーメント(曲げる力)が
ほとんどかからないように設計されています。
それぞれの棒が「引っ張られる」か「押される」かの
どちらかだけを受け持つため、力の解析がシンプルで、
構造全体が軽量で済むというメリットがあります。
なぜトラスには曲げモーメントがかからないのか?
そもそも曲げモーメントってなに?
「曲げモーメント」とは、部材をグイッと曲げようとする力のことです。
これは、端を固定して反対側に力をかけるようなときに発生します。
🔍 例)
こういう状態が曲げモーメントがかかっている状態です。
トラス構造では曲げが「起こらない設計」になっている!
トラス構造の部材の接続部分(節点)は、
基本的に「ヒンジ(回転自由)」で設計されます。
このヒンジは、力がかかっても回転して逃げるので、
「固定された棒のように曲がること」がありません。
🔍 つまり
- 曲げようとしても回るだけで曲げ力が発生しない
- だからその部材は引っ張るか押すかの直線的な力だけを受ける
というわけです。
イメージ図で考えてみよう
- 固定された棒に力を加えると
→ 曲がろうとする → 曲げモーメントがかかる - ヒンジでつながった棒に力を加えると
→ ヒンジが回転して逃がす → 曲げがかからない
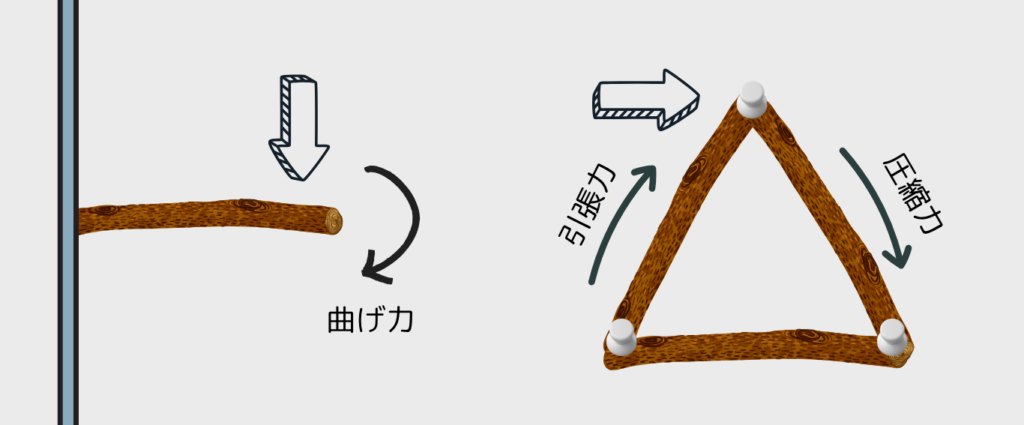
引張力・圧縮力に限定されるから、解析がラク&構造が軽い!
トラスは、曲げ力がかからない代わりに
「引張力」か「圧縮力」だけで部材が構成されます。
だから構造解析も簡単で、
軽量でも強い構造が実現できるのです。
| 項目 | 内容 |
|---|---|
| 曲げモーメントとは? | 部材を曲げようとする力(竿がしなるような力) |
| なぜトラスにはかからない? | 節点がヒンジ接合(回転自由)だから、曲げが逃げる |
| どんな力がかかる? | 引張力(引っ張る)と圧縮力(押す)だけ |
| その結果どうなる? | 力の流れが単純、構造が軽くて強い |
トラス構造は、「曲げずに支える」ための頭のいい設計です!
だから細くて軽い部材でも、びっくりするほど頑丈にできるんです。
トラス構造のメリットまとめ
トラス構造が強く、さまざまな現場で使われる
理由をまとめると、次のようになります。
メリット一覧
| メリット | 内容 |
|---|---|
| 高い剛性(変形しにくい) | 三角形の安定性により力を受けても形が保たれる |
| 軽量でも高強度 | 部材に曲げがかからず、細くても強い |
| 材料を節約できる | 無駄がなく、必要最小限の部材で構成可能 |
| 製造・組立が容易 | 単純な棒材の組み合わせで作れる |
| 力の解析がしやすい | 引張と圧縮のみを考慮すればよい |
機械設計におけるトラス構造の応用例
トラス構造は建築分野だけでなく、機械設計の世界でも大活躍しています。
応用例
ロボットアームの支柱
自転車やバイクのフレーム
航空機の胴体部構造
フレーム溶接構造の軽量化
FEA解析での剛性検討

設計者が「軽くて強く、変形しない構造」を目指すと、
自然とトラス構造の考えにたどり着くのです。
注意点:トラス構造にも弱点がある?
もちろん万能というわけではありません。
以下のような点には注意が必要です。
トラス構造の弱点
| 注意点 | 内容 |
|---|---|
| 座屈のリスク | 圧縮部材が長すぎると折れてしまう可能性あり |
| 接合部の設計が重要 | ジョイント部の剛性や精度が構造全体に影響 |
| 部材の本数が増える | 複雑になりやすく、加工・組立コストが上がることも |
| 剛性過剰のリスク | 不要な強度過剰により逆にコスト・重量増になる |
これらの点をふまえて、「どの場面にトラス構造を使うのか」を判断することが、
機械設計者としての重要なスキルとなります。
まとめ|三角形は最強の構造要素!
最後に一言|「軽くて強い構造」を考え始めたら、まず三角形を思い出そう
機械設計の現場では、
剛性・軽量化・コストのバランスを取ることが常に求められます。
そんなとき、トラス構造の考え方を取り入れることで、
「軽くて壊れにくい設計」がぐっと近づきます。
部品の配置、筐体フレーム、治具の支持構造――
ぜひ、三角形とトラス構造の原理を、あなたの設計に活かしてください!



















コメント