～動力選定で加減速を見落とすと危険！～
機械設計で「ステージを何秒で移動させたい」「一定時間で物を運びたい」といった動作時間の要件を満たすために、必要なモーターの回転数や出力（動力）を選定する場面があります。
そのとき、よく使うのが「移動距離 ÷ 時間 = 平均速度」の計算です。
でもこの「平均速度」だけで選定するのは危険です。
なぜなら、実際の動きは必ず「加速・減速の区間があるから」です。
この記事では、平均速度と最大速度の違い・注意点・設計のポイントを、初心者にもわかりやすく解説します。
平均速度とは？
平均速度とは、「移動距離を全体の移動時間で割った値」です。
🔍 例）
100mmを0.2秒で移動する場合
▶ 平均速度 = 100mm ÷ 0.2s = 500mm/s
これはあくまで「全体として見たときの平均値」であり、
実際にずっと500mm/sで動いているわけではありません。
実際はどう動くの？
現実のモーターやアクチュエーターは、いきなり最大速度で動いたり、急に止まったりはできません。
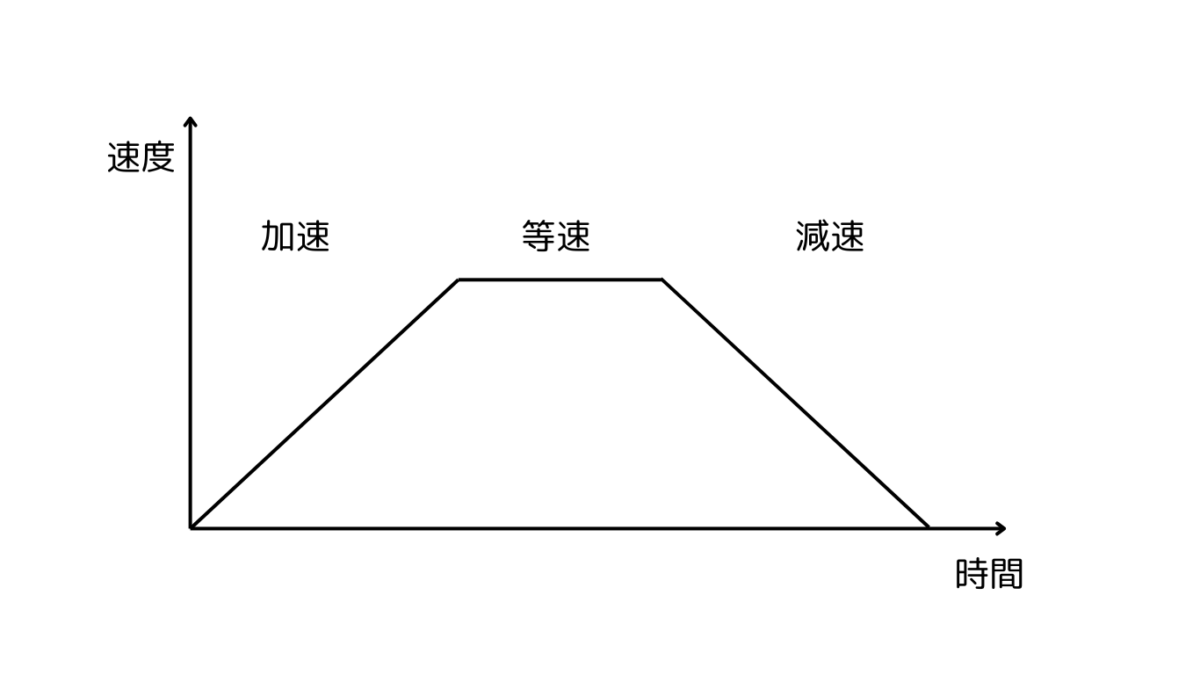
物理的には「加速区間・等速区間・減速区間」の3つで構成されます。
等加速度運動のイメージ
- 最初はゆっくり速度を上げ
- 真ん中で一定速度（＝最大速度）
- 最後に滑らかに停止する
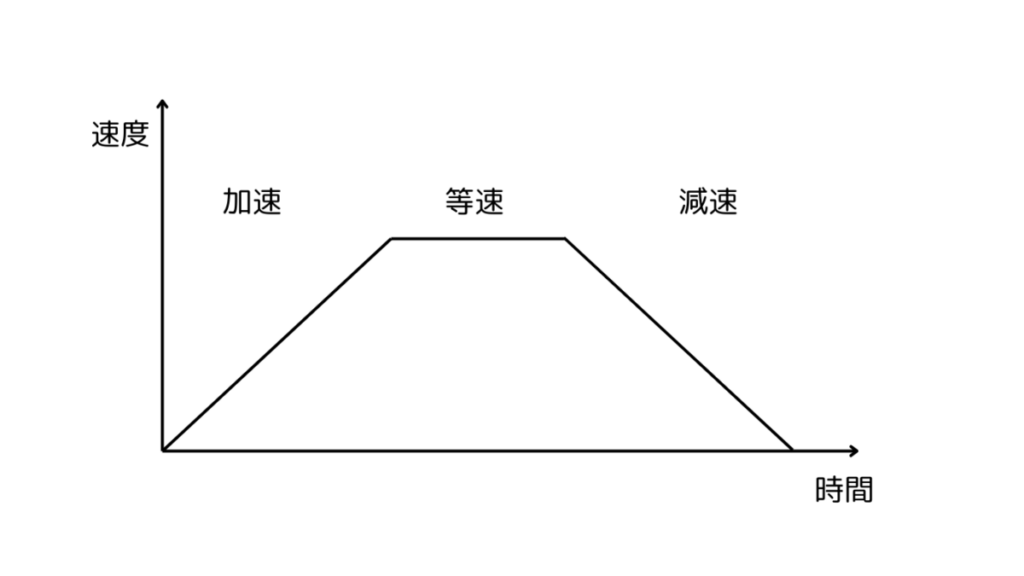
最大速度は平均速度より「高くなる」！
加減速の時間を含むと、実際に一定速度で動ける時間が短くなります。
そのため、目標の時間内に移動を終えるには、途中の最大速度を速くしなければならないのです。
計算例①（等加速度運動を仮定）
- 総移動距離：100mm
- 総移動時間：0.2秒
- 加速時間：0.05秒
- 減速時間：0.05秒
- 等速時間：0.1秒
最大速度の計算①
「加減速が等加速度運動」であることを前提として、以下のステップで最大速度（Vmax）を求めます。
ステップ①：各区間の移動距離を求める
✅ 加速区間（0 → Vmax、時間 0.05秒）
等加速度運動の移動距離は下記の式で求めます。
\( \displaystyle x=\frac{1} {2}at^2\)
- aは加速度
- tは時間
\( \displaystyle a（加速度）=\frac{Vmax} {t} なので、\)
\( \displaystyle x(加速)=\frac{1} {2}・\frac{Vmax} {t}・t^2=\frac{1} {2}Vmax・t\)
\( \displaystyle x(加速)=\frac{1} {2}Vmax・0.05\)
✅ 減速区間も同様（対称なので）
\( \displaystyle x(減速)=\frac{1} {2}Vmax・0.05\)
✅ 等速区間（時間 0.1秒）
\( \displaystyle x(等速)=Vmax・0.1\)
ステップ②：全体の距離を合計する
\( \displaystyle x(合計)=x（加速)+x(等速)+x(減速)\)
\( \displaystyle x=\frac{1} {2}Vmax・0.05+Vmax・0.1+\frac{1} {2}Vmax・0.05\)
\( \displaystyle x=Vmax・(0.025+0.1+0.025)=Vmax・0.15\)
ステップ③：移動距離 100mm を代入して解く
\( \displaystyle 100=Vmax・0.15\)
\( \displaystyle Vmax=\frac{100} {0.15}=666.67mm/s\)
計算例②（等加速度運動を仮定）
- 総移動距離：100mm
- 総移動時間：0.2秒
- 加速時間：0.1秒
- 減速時間：0.05秒
- 等速時間：0.05秒
計算例①より加速を遅くすると、最大速度がどの程度変化するか計算してみます。
最大速度の計算②
「加減速が等加速度運動」であることを前提として、以下のステップで最大速度（Vmax）を求めます。
ステップ①：各区間の移動距離を求める
✅ 加速区間（0 → Vmax、時間 0.1秒）
等加速度運動の移動距離は下記の式で求めます。
\( \displaystyle x=\frac{1} {2}at^2\)
- aは加速度
- tは時間
\( \displaystyle a（加速度）=\frac{Vmax} {t} なので、\)
\( \displaystyle x(加速)=\frac{1} {2}・\frac{Vmax} {t}・t^2=\frac{1} {2}Vmax・t\)
\( \displaystyle x(加速)=\frac{1} {2}Vmax・0.1\)
✅ 減速区間（Vmax →0、時間 0.05秒）
\( \displaystyle x(減速)=\frac{1} {2}Vmax・0.05\)
✅ 等速区間（時間 0.05秒）
\( \displaystyle x(等速)=Vmax・0.05\)
ステップ②：全体の距離を合計する
\( \displaystyle x(合計)=x（加速)+x(等速)+x(減速)\)
\( \displaystyle x=\frac{1} {2}Vmax・0.1+Vmax・0.05+\frac{1} {2}Vmax・0.05\)
\( \displaystyle x=Vmax・(0.05+0.05+0.025)=Vmax・0.125\)
ステップ③：移動距離 100mm を代入して解く
\( \displaystyle 100=Vmax・0.125\)
\( \displaystyle Vmax=\frac{100} {0.125}=800mm/s\)
加速が遅くなった分、最高速度が高くなることがわかります。
加減速と最高速度の関係
| 移動距離 | 加速時間 | 等速時間 | 等速時間 | 最高速度 |
| 100ｍｍ | 0.05ｓ | 0.1ｓ | 0.05ｓ | 666.67ｍｍ/ｓ |
| 100ｍｍ | 0.1s | 0.05ｓ | 0.05ｓ | 800ｍｍ/ｓ |
| 100ｍｍ | 0.1s | 0s | 0.1s | 1000mm/s |
加減速時間と最高速度・必要トルクの関係をわかりやすく解説！
機械設計やモーター選定を行う際に、「加減速時間をどう設定するか」はとても重要なポイントです。
特に「最高速度」と「必要トルク（加減速時の負荷）」に大きく関係します。
加減速時間が長くなると、最高速度は上がる
例えば、「移動距離100mm、動作時間0.2秒」という条件で、加減速にたっぷり時間をかける（たとえば0.1秒ずつ）とどうなるでしょうか？
- 加減速時間が長くなる＝なだらかに加速・減速する
- 等速で動ける時間が短くなる、もしくはゼロになる
- 移動時間内で距離を稼ぐために、より高い速度（Vmax）が必要になる
つまり、加減速が長いと「ゆっくり始まり、ゆっくり止まる」かわりに、途中でより速く走る必要があるんですね。
📝 イメージ
- ゆっくり踏み込んで、ゆっくりブレーキ 👉 そのぶん真ん中でスピード出さなきゃ距離を稼げない！
加減速時間が短くなると、必要トルクが増える
逆に、加減速にかける時間を短くすると、こうなります。
- 短い時間で一気に加速・減速
- 加速度が大きくなる
- 必要なトルク（慣性に打ち勝つための力）が大きくなる
加速時に必要なトルクは以下の式で決まります。
\( \displaystyle T=J・a\)
- T：トルク（N·m）
- J：回転体の慣性モーメント（kg·m²）
- α：角加速度（rad/s²）
つまり、加速を速くする（＝αを大きくする）と、トルクが跳ね上がるということです。
これは電動アクチュエーターやサーボモーターにとって大きな負担になります。
設計上のバランスが大事！
| 加減速時間 | 特徴 | メリット | デメリット |
|---|---|---|---|
| 長くする | なだらかな動き | 機械にやさしい、トルクが小さい | 最高速度が高くなる （制御・選定に注意） |
| 短くする | 急な動き | 移動時間が短縮できる | トルク負荷が大きい 機器に負担がかかる |
動作プロファイルのバランスが大切。モーター性能や構造部品の強度を考慮して調整するのがポイント！
加減速時間が長いと、なだらかに動く代わりに最高速度が必要になる
加減速時間が短いと、急に動くため大きなトルクが必要になる
滑らかな加減速が必要な場合の注意点
最近の装置では、
- 製品や材料を傷つけない
- 精密な動きを実現する
- ロボットや人との協調を行う
といった理由で「滑らかな加減速（S字加減速など）」が求められます。
このときのポイント
- 滑らかに加減速する＝加速にかかる時間が長くなる
- 等速で動ける時間が短くなる
- 目的の時間内に移動するには、さらに速い最大速度が必要になる！
平均速度は同じでも、加減速の仕方によって最大速度は変わるのが重要なポイントです！
動力（トルク・出力）選定への影響
モーターの出力トルクや電流は、最大速度や最大加速度に応じて増加します。
例：加速度から必要トルクを求める（慣性負荷あり）
- 必要トルク = 負荷慣性 × 加速度
加速度が大きくなると、必要トルクが急激に増加します。
つまり、加速を早く・スムーズにしようとすると、それに見合った強いモーターが必要になるのです。
平均速度と最大速度をどう使い分ける？
| 項目 | 内容 | 使用シーン |
|---|---|---|
| 平均速度 | 総移動距離 ÷ 時間 | ざっくりした目安や時間評価に使う |
| 最大速度 | 実際の動作時に到達する最高速 | 正確な動力・トルクの計算に必要 |
| 加速度 | 最高速までにかかる時間 | トルク・電流値・滑らかさの調整に重要 |
設計のポイント
- 平均速度だけで動力選定しない
- 必ず加速・減速の時間を考慮する
- 滑らかな動作（S字加減速）をする場合は最高速度がさらに上がる
- 必要トルクは小さくなるが、最大速度能力に注意。
- 加減速時間を明確に設計図面や仕様書に明記する
- モーションプログラムでも必須
- 安全率を見込んで、余裕のあるモーター・減速機を選ぶ
まとめ
✔ 平均速度と最大速度は違う！
✔ 実際のモーションには「加速・減速」があることを忘れない
✔ 滑らかな加減速では、設計上の最大速度がより大きく必要
✔ 動力選定は「速度」だけでなく、「加速度」も見ることが成功のカギ！
「とりあえず平均速度で選んだけど、実際は全然足りなかった…」という失敗はとても多いです。
動きの中身をちゃんと見て、動力選定を「平均」ではなく「動作の実態」で考えることが、良い設計への第一歩です！
コメント