機械設計において、梁（はり）の剛性やたわみを考慮することは、
構造物や機械部品の安全性と性能を確保するために非常に重要です。
特に材料選定では、強度や剛性の違いが部品のたわみ量に直接影響します。
この記事では、機械設計でよく使用される2つの材料、
SS400（一般構造用鋼材）とA5052（アルミニウム合金）の剛性について、
はりのたわみという観点から比較します。
材料特性の概要
まず、SS400とA5052の基本的な材料特性を確認します。
SS400（一般構造用圧延鋼材）
ヤング率（剛性の指標）
\( \displaystyle 約205GPa=205000MPa\)
🔍 密度
\( \displaystyle 約7.86ｇ/cm^3=7.86×10^-6kg/mm^3\)
👉 主な用途
建築構造、機械部品、フレーム構造など
A5052（アルミニウム合金）
ヤング率（剛性の指標）
\( \displaystyle 約70GPa=70000MPa\)
🔍 密度
\( \displaystyle 約2.68ｇ/cm^3=2.68×10^-6kg/mm^3\)
👉 主な用途
軽量構造部品、航空機、船舶、自動車部品など
ヤング率による剛性の比較
剛性（材料の固さや変形しにくさ）は、主に材料のヤング率によって決まります。
ヤング率は、材料に対する応力とそれに伴うひずみ（変形量）の関係を示す値であり、
数値が大きいほど材料は変形しにくく、剛性が高いことを意味します。
- SS400のヤング率
- 約205 GPa
- A5052のヤング率
- 約70 GPa
この値からわかるように、SS400はA5052に比べて剛性が約3倍高いです。
同じ形状や荷重条件で比較した場合、
A5052の方がSS400よりも大きくたわむことが予想されます。
はりのたわみ計算
次に、はりに対するたわみを計算して、
2つの材料の剛性差を定量的に見ていきます。
たわみの計算には、
材料のヤング率と断面二次モーメントを用いて次の式を使います。
ヤング率の違いからどの程度違いがでるのか、実際に計算していきます。
梁の条件設定
今回の計算に用いる条件は以下の通りです。
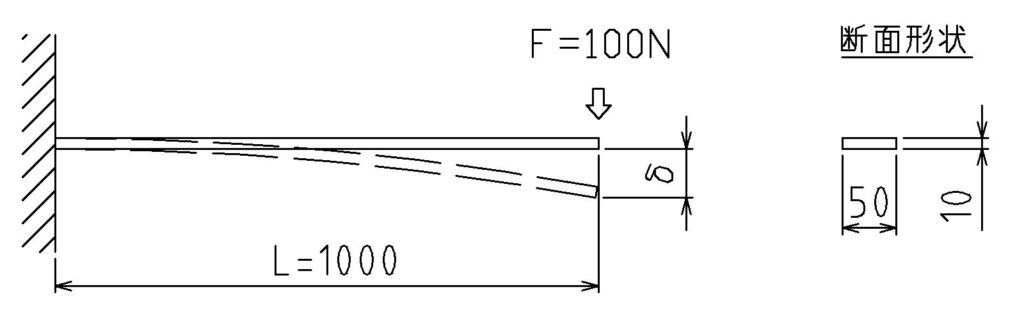
- 梁の長さ L=1000 mm
- 荷重 F=100 N
- 断面は幅50mm、高さ10mmの矩形断面
- 断面二次モーメント I
- \( \displaystyle I=\frac{bh^3} {12}=\frac{50×10^3} {12}=4166.7mm^4\)
これをもとに、SS400とA5052のたわみをそれぞれ計算します。
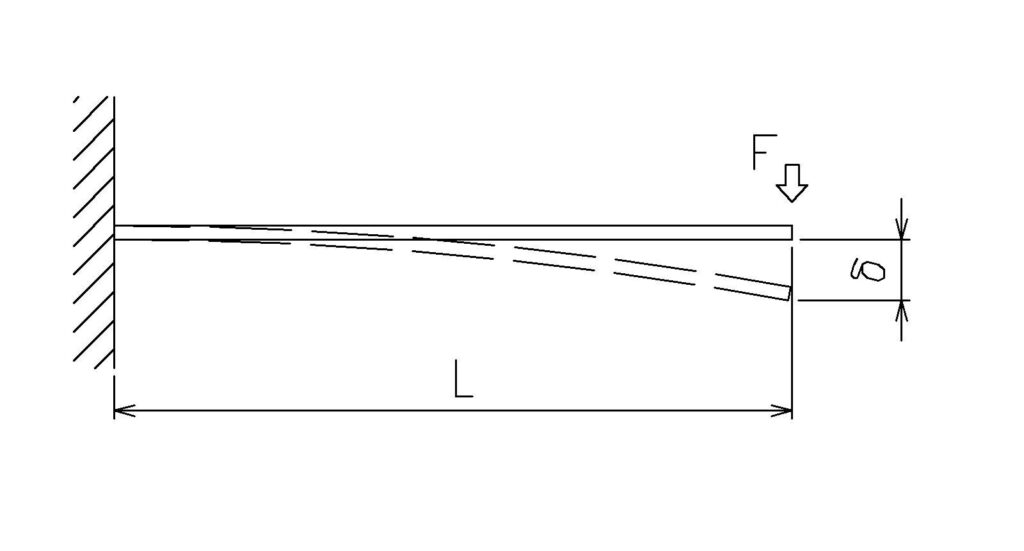
片持ち梁のたわみ計算式（集中荷重の場合）
片持ち梁に集中荷重が先端にかかる場合のたわみは次の式で計算されます。
\( \displaystyle δF=\frac{FL^3} {3EI}\)
- δF：たわみ量（mm）
- F：荷重（N）
- L：梁の長さ（mm）
- E：ヤング率（N/mm²）
- I：断面二次モーメント（mm⁴）
片持ち梁の自重によるたわみ計算
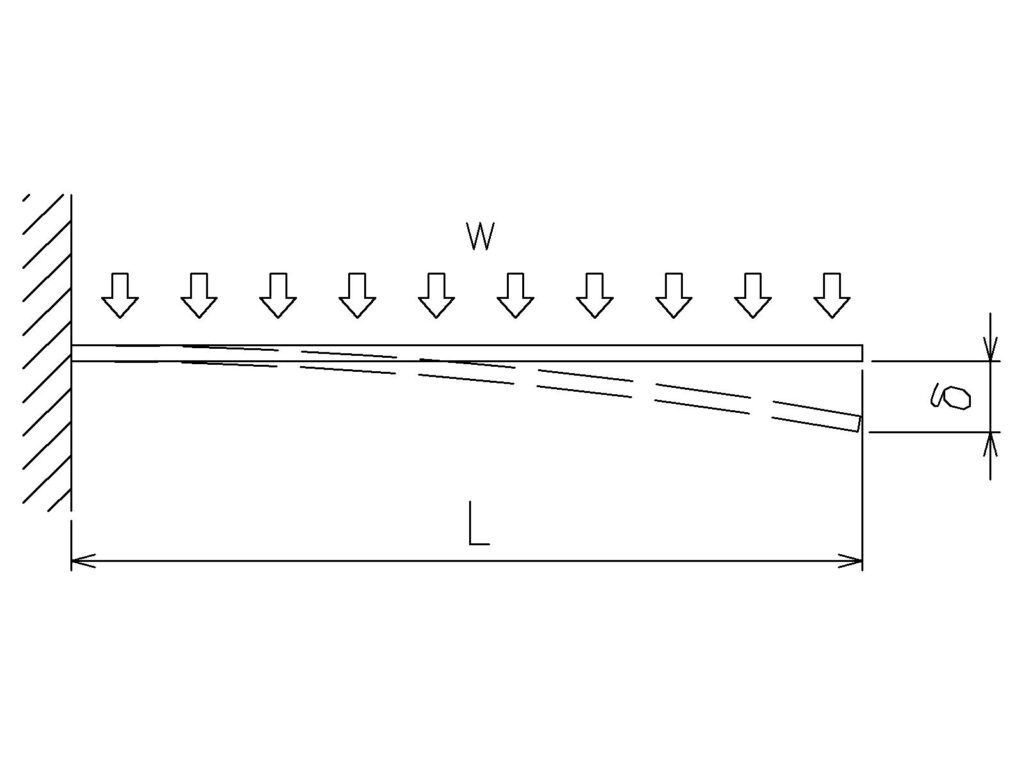
はり自身の重さによるたわみは、均等分布荷重として扱います。
片持ち梁に均等分布荷重 w がかかる場合のたわみは次の式で求められます。
\( \displaystyle δw=\frac{wL^4} {8EI}\)
- δw：自重によるたわみ量（mm）
- w：単位長さあたりの荷重（N/mm）
- L：梁の長さ（mm）
- E：ヤング率（N/mm²）
- I：断面二次モーメント（mm⁴）
- g:kg⇒N 換算（9.8とする）
\( \displaystyle w=密度(kg/㎣)×断面積(㎟)×g(9.8)\)
総たわみの計算
総たわみ量は、集中荷重によるたわみと自重によるたわみの合計となります。
\( \displaystyle δtotal=δF+δw\)
SS400とA5052のたわみ計算比較
SS400の場合のたわみ計算
SS400のヤング率E=205GPa(205000N/㎟)を代入して、たわみを計算します。
集中荷重によるたわみ
\( \displaystyle δF=\frac{FL^3} {3EI}\)
上記の式に数値を代入します。
\( \displaystyle δF=\frac{100×1000^3} {3×205000×4166.7}\)
これを計算すると、
\( \displaystyle δF=39.02mm\)
自重によるたわみ
まずはwの計算
\( \displaystyle w=密度(kg/㎣)×断面積(㎟)×g(9.8)\)
上記の式に数値を代入します。
\( \displaystyle w=7.86×10^-6(kg/㎣)×50×10(㎟)×g(9.8)\)
これを計算すると ｗ＝0.0385
\( \displaystyle δw=\frac{wL^4} {8EI}\)
上記の式に数値を代入します。
\( \displaystyle δw=\frac{0.0385×1000^4} {8×205000×4166.7}\)
これを計算すると
\( \displaystyle δｗ=5.63mm\)
総たわみ
\( \displaystyle δtotal=δF+δw\)
\( \displaystyle δtotal=39.02+5.63＝44.65mm\)
A5052の場合のたわみ計算
同様にA5052のたわみ計算をします。
A5052のヤング率E=70GPa(70000N/㎟)を代入して、たわみを計算します。
集中荷重によるたわみ
\( \displaystyle δF=\frac{100×1000^3} {3×70000×4166.7}\)
これを計算すると、
\( \displaystyle δ=114.29mm\)
自重によるたわみ
まずはwの計算
\( \displaystyle w=2.68×10^-6(kg/㎣)×50×10(㎟)×g(9.8)\)
これを計算すると ｗ＝0.0131
\( \displaystyle δw=\frac{0.0131×1000^4} {8×70000×4166.7}\)
これを計算すると
\( \displaystyle δｗ=5.61mm\)
総たわみ
\( \displaystyle δtotal=114.29+5.61＝119.9mm\)
剛性比較の結果
SS400の場合の総たわみ
➤ 約44.65ｍｍ
A5052の場合の総たわみ
➤ 約119.9ｍｍ
これらの計算から、
A5052の方がSS400よりも約2.7倍のたわみを示すことがわかります。
これは、A5052のヤング率がSS400の約1/3であり、
同じ荷重条件下での剛性が低く、たわみが大きくなることを示しています。
ヤング値とたわみの関係を感覚的に覚えて最適な設計を効率よく進めよう！
軽量化と剛性のバランス
A5052は剛性の面ではSS400に劣りますが、
軽量化が求められる場面では非常に有利です。
例えば、自動車や航空機などの構造では、
軽量化によって燃費や性能を向上させることが可能です。
A5052の密度はSS400の約1/3であるため、
質量あたりの剛性を考慮した設計が重要です。
設計への応用
たわみの許容範囲を満たすためには、以下のような対策が考えられます。
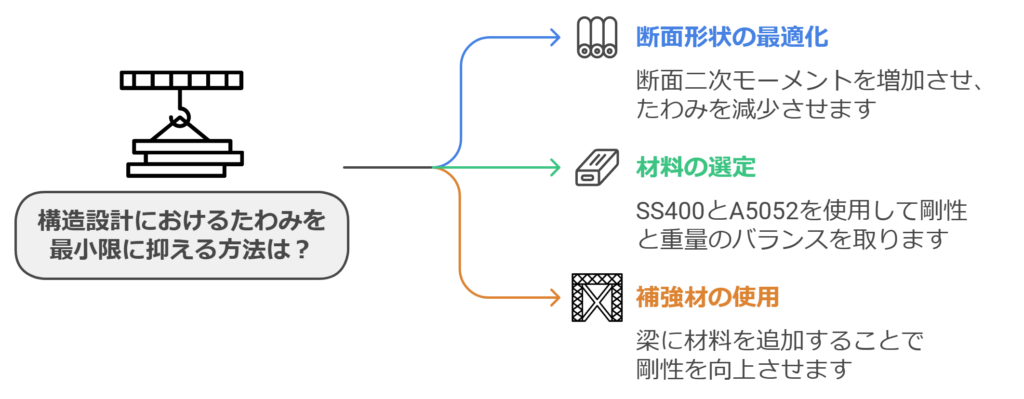
断面形状の最適化
A5052を使用する場合、断面形状をI型や中空形状にすることで、
断面二次モーメントを増加させ、たわみを抑えることができます。
材料の選定
剛性が必要な部分にはSS400を、
軽量化が求められる部分にはA5052を適切に組み合わせることで、
全体のバランスを取ります。
補強材の使用
A5052の梁に補強材を追加することで、剛性を向上させることも可能です。
まとめ
SS400とA5052の剛性を比較すると、
SS400の方が明らかに剛性が高く、たわみが小さいことがわかります。
しかし、設計の際には剛性だけでなく、
軽量化や耐食性、コストなど他の要素も考慮する必要があります。
特に、軽量化を重視する設計では、
たわみの増加を許容範囲内に収めるために断面形状を工夫することが求められます。
機械設計においては、使用する材料の特性をよく理解し、
用途に応じて適切な材料と断面形状を選定することで、
安全性と効率性を両立させた最適な設計を実現することができます。
これにより、製品の性能向上やコスト削減も達成可能となります。
設計において欠かせない材料の特性や用途を解説しています。
適材適所の選定をサポートします。
コメント